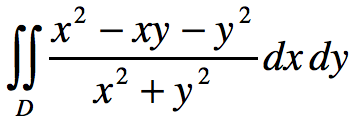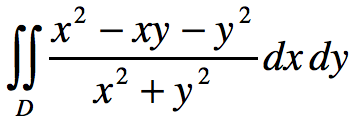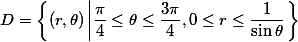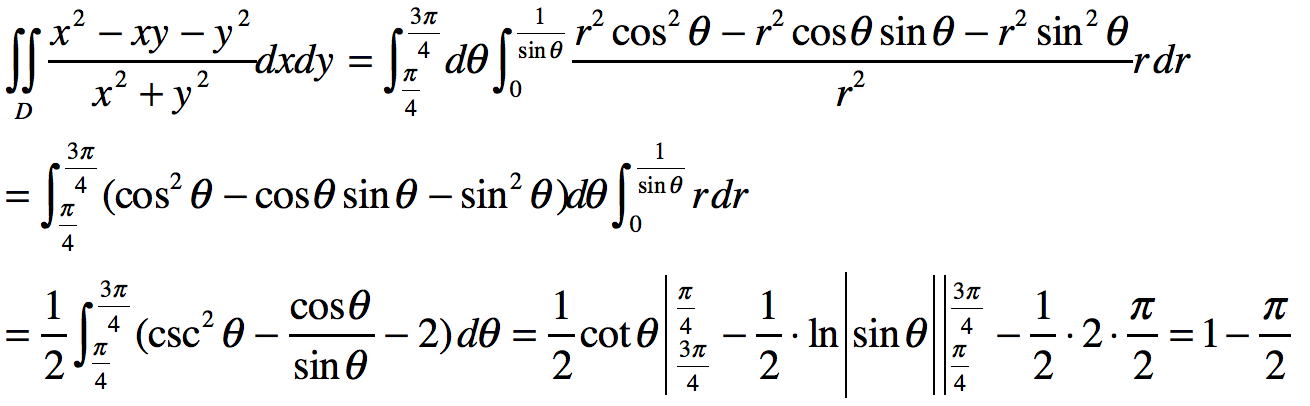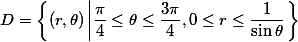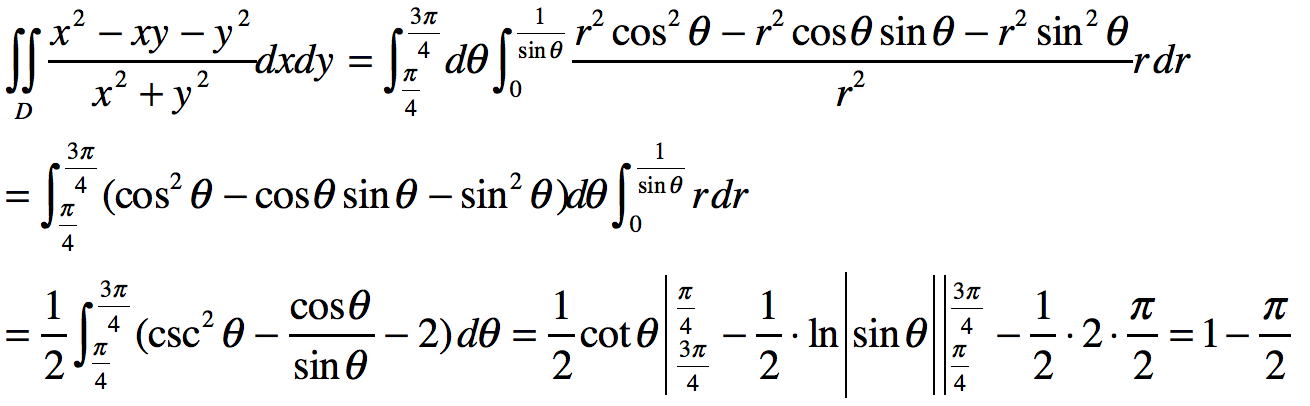考题
设(X,Y)服从在区域D上的均匀分布,其中D为x轴、y轴及x+y=1所围成,求X与Y的协方差Cov(X,Y).
考题
设平面区域D由曲线y=1/x及直线y=0,x=1,x=е2所围成,二维随机变量(X,Y)在区域D上服从均匀分布,则(X,Y)的联合密度函数为()。
考题
计算二重积分,其中D是由直线y=x,x=1以及x轴所围的区域.
考题
若D是由x轴、y轴及直线2x+y-2=0所围成的闭区域,则二重积分
的值等于( )A.1
B.2
C.1/2
D.-1
考题
Ω是由曲面z=x2+y2,y=x,y=0,z=1在第一卦限所围成的闭区域,f(x,y,z) 在Ω上连续,则等于:
考题
由曲线和直线x=1,x=2,y= -1围成的图形,绕直线:y= -1旋转所得旋转体的体积为:
考题
由曲线y=ex,y=e-2x及直线x=-1所围成图形的面积是:
考题
若D是由x=0,y=0,x2+y2=1所围成在第一象限的区域,则二重积分
等于( )。
考题
设平面闭区域D由x=0,y=0,x+y=1/2,x+y=1 所围成。
A.I123 B. I132
C. I321 D. I312
考题
由曲线y=x2/2和直线x=1,x=2,y=-1围成的图形,绕直线y=-1旋转所得旋转体的体积为:
A.(293/60)π B.π/60 C. 4π2 D. 5π
考题
由曲线y=x3,直线x=1,z轴围成的平面有界区域的面积为_________.
考题
计算二重积分,其中积分区域D是由x=0、x=1、y=0、y=1所围成的闭区域
考题
设f(x,y)为连续函数,且满足,其中D是由x轴、y轴、所围成的闭区域
考题
请计算,其中D是由y=1/x=2,y=x所围成的闭区域
考题
请计算二重积分,其中D是由圆周、x轴,y轴所围成的在第一象限内的闭区域
考题
设二维随机变量(X,Y)服从区域G上的均匀分布,其中G是由x-y=0,x+y=2,与y=0所围成的三角形区域.
(Ⅰ)求X的概率密度fx(x);
(Ⅱ)求条件概率密度.
考题
设Ω是由平面x+y+z=1与三个坐标平面所围成的空间区域,则=_________.
考题
设平面闭区域D由x=0,y=0,x+y=1/2,x+y=1 所围成。
A.I123
B. I132
C. I321
D. I312
考题
在平面有界区域内,由连续曲线C围成一个封闭图形。证明:存在实数ξ使直线y=x+ξ平分该图形的面积。
考题
设区域D是由直线y=x,x=2,y=1围成的封闭平面图形,
考题
,其中区域如图5-3所示,由y=x,y=1与Y轴围成.
考题
求由曲线y=x2(x≥0),直线y=1及Y轴围成的平面图形的面积·
考题
设D为曲线y=x2与直线y=x所围成的有界平面图形,求D绕x轴旋转一周所得旋转体的体积V.?
考题
计算二重积分
,其中D是由直线
及y=1围
成的平面区域.
考题
由曲线y=x2/2和直线x=1,x=2,y=-1围成的图形,绕直线y=-1旋转所得旋转体体积为:()A、(293/60)πB、π/60C、4π2D、5π
考题
设(X,Y)在由直线y=x,y=2-x,y=0所围的区域内服从均匀分布,则P{0.1
考题
单选题由曲线y=x2/2和直线x=1,x=2,y=-1围成的图形,绕直线y=-1旋转所得旋转体体积为:()A
(293/60)πB
π/60C
4π2D
5π