网友您好， 请在下方输入框内输入要搜索的题目：
题目内容
（请给出正确答案）
设总体X～N(0,8),Y～N(0,2^2),且及(Y1,Y2)分别为来自上述两个总体的样本,则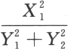
～_______.
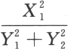～_______.参考答案
参考解析
解析：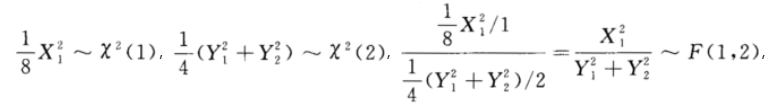
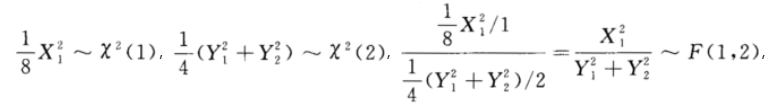
更多 “设总体X～N(0,8),Y～N(0,2^2),且及(Y1,Y2)分别为来自上述两个总体的样本,则～_______.” 相关考题
考题
已知“a=dict(x=1,y=dict(y1=2,y2=3))”且“b=a.copy()”,则执行“a['y']['y1']=10”后,则print(b)的输出结果为()。
A、{x=1,y={y1=10,y2=3}}B、{x=1,y={y1=2,y2=3}}C、{'x':1,'y':{'y1':10,'y2':3}}D、{'x':1,'y':{'y1':2,'y2':3}}
考题
【程序】SET TALK OFFCLEARINPUT“N=”TO NINPUT“M=”TO MX=MIN(N，M)FOR I＝X TO 1 STEP -1IF M/I＝INT(M/I)AND N/I=INT(N/I)Y1=IEXITENDIFENDFOR?“Y1=”+ALLTRIM(STR(Y1，19))+“，Y2＝”+ALLTRIM(STR(M，N)/Y1，19))SET TALK ON若输入N、M的值分别为6，8，则Y1的输出结果为 ______。A．0B．1C．2D．3
考题
设非齐次线性微分方程y′+P(x)y=Q(x)有两个不同的解y1(x)，y2(x)，C为任意常数，则该方程通解是( )。A.C[y1(x)-y2(x)]
B.y1(x)+C[y1(x)-y2(x)]
C.C[y1(x)+y2(x)]
D.y1(x)+C[y1(x)+y2(x)]
考题
设非齐次线性微分方程y+P(x)y=Q(x)有两个不同的解析：y1(x)与y2(x)，C为任意常数，则该方程的通解是( ).A.C[(y1(x)-y2(x)]
B.y1(x)+C[(y1(x)-y2(x)]
C.C[(y1(x)+y2(x)]
D.y1(x)+C[(y1(x)+y2(x)]
考题
设总体X～B(m，θ)，X1，X2，…，Xn为来自该总体的简单随机样本，X为样本均值，则=A.(m-1)nθ(1-θ).
B.m(n-1)θ(1-θ).
C.(m-1)(n-1)θ(1-θ).
D.mnθ(1-θ).
考题
设X1,X2,X3,X4,X5为来自正态总体X～N(0,4)的简单随机样本,y=a（X1-2X2）^2+b(3X3-4X3)^2+(abc≠o),且y～χ^2（n）,则a=_______,b=_______,c=_______,b=_______.
考题
两线性时不变离散时间系统分别为S1和S2，初始状态均为零。将激励信号f（n）先通过S1再通过S2，得到响应y1（n）；将激励信号f（n）先通过S2再通过S1，得到响应y2（n）。则y1（n）与y2（n）的关系为（）
考题
单选题设非齐次线性微分方程y′＋P（x）y＝Q（x）有两个不同的解y1（x），y2（x），C为任意常数，则该方程的通解是（ ）。A
C[y1（x）－y2（x）]B
y1（x）＋C[y1（x）－y2（x）]C
C[y1（x）＋y2（x）]D
y1（x）＋C[y1（x）＋y2（x）]
考题
填空题已知Y1服从N（12， 12），Y2服从N（10， 22），当以n1=n2=8抽样时，两个样本平均数差数y1-y2服从N（）
热门标签
最新试卷