网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设封闭曲线L的极坐标方程为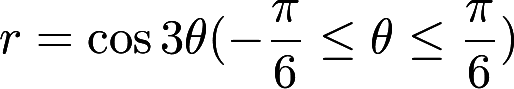 ,则L所围成的平面图形的面积为
,则L所围成的平面图形的面积为
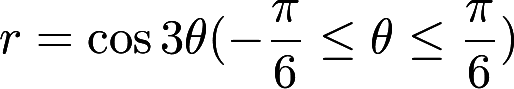 ,则L所围成的平面图形的面积为
,则L所围成的平面图形的面积为参考答案
参考解析
解析: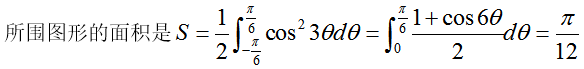
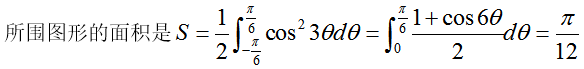
更多 “设封闭曲线L的极坐标方程为,则L所围成的平面图形的面积为” 相关考题
考题
(1)求直线y=1,曲线L以及y轴围成的平面图形绕y轴旋转一周所得到的的旋转体体积A;(2)假定曲线L绕y轴旋转一周所得到的旋转曲面为S。该旋转曲面作为容器盛满水(水的质量密度(单位体积水的重力)等于1),如果将其中的水抽完,求外力作功W.
考题
蓄电池充电曲线和放电曲线所围成的封闭图形面积的物理意义是蓄电池充电时的电能消耗。
热门标签
最新试卷