网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
已知P为抛物线y2=x的焦点,点M,N在该抛物线上且位于x轴的两侧,

(其中O为坐标原点),则ΔMPO与ΔNPO面积之和的最小值是( )。
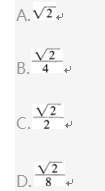

(其中O为坐标原点),则ΔMPO与ΔNPO面积之和的最小值是( )。
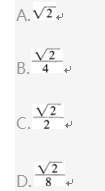
参考答案
参考解析
解析:设直线
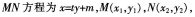
直线方程与抛物线方程联立,可得
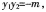
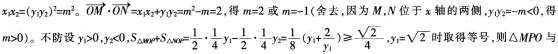
△NPO面积之和的最小值是

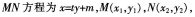
直线方程与抛物线方程联立,可得
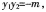
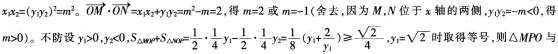
△NPO面积之和的最小值是

更多 “已知P为抛物线y2=x的焦点,点M,N在该抛物线上且位于x轴的两侧, (其中O为坐标原点),则ΔMPO与ΔNPO面积之和的最小值是( )。 ” 相关考题
考题
如图所示,已知A,B为直线L:y=mx-m+2与抛物线y=x2的两个交点。
(1)直线ι经过一个定点C,试求出点C的坐标;(2分)
(2)若m=-1,已知在直线L下方的抛物线上存在一点P(点P与坐标原点0不重合),且△ABP的面积为(3√13)/2,求点P的坐标。(6分)
考题
以抛物线y2=8x的焦点为圆心,且与此抛物线的准线相切的圆的方程是( )A.(x+2)2+y2=16
B.(x+2)2+y2=4
C.(x-2)2+y2=16
D.(x-2)2+y2=4
考题
单选题过抛物线y=4x的焦点,作直线与此抛物线相交于两点P和Q,那么线段PQ中点的轨迹方程()A
y=2x-1B
y=2x-2C
y=-2x+1D
-2x+2
热门标签
最新试卷