网友您好， 请在下方输入框内输入要搜索的题目：

题目内容 （请给出正确答案）
过抛物线y2=4x的焦点，作直线与此抛物线相交于两点P和Q，那么线段PQ中点的轨迹方程是（　　）．

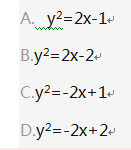
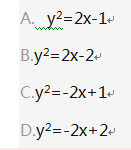
参考答案

参考解析
解析：(筛选法)由已知可知轨迹曲线经过点(1，0)，开口向右，由此排除答案A、C、D，所以选B.
更多 “过抛物线y2=4x的焦点，作直线与此抛物线相交于两点P和Q，那么线段PQ中点的轨迹方程是（　　）． ” 相关考题
考题 已知过点（0，4），斜率为-1的直线l与抛物线C：y2—2px（b&gt；0）交于A，B两点．（I）求C的顶点到2的距离；（Ⅱ）若线段AB中点的横坐标为6，求C的焦点坐标．
查看答案
考题 抛物线y2=-4x的准线方程为 （ ）A.x=-1B.x=1C.y=1D.Y=-l
查看答案
考题 （2） 设点P是椭圆C的左准线与 x轴的交点，过点P的直线L与椭圆C相交于M.N两点，当线段MN的中点落在正方形Q内（包括边界）时，求直线L的斜率的取值范围。
查看答案
考题 已知A,B是抛物线y2=4x上的两个动点,且|AB|=3,则当AB的中点M到y轴的距离最短时,点M的横坐标是____.
查看答案
考题 抛物线y2=3x的准线方程为 （ ）A.AB.BC.CD.D
查看答案
考题 已知双曲线C：x2/a2-y2/b2=1(a>0，b>0)的一个焦点是抛物线y2=8x的焦点，且双曲线C的离心率为2，那么双曲线C的方程为_______。
查看答案
考题 (1)求椭圆的标准方程； (2)F2为椭圆的右焦点，过椭圆的中心作一条倾斜角为45°的直线与椭圆交于A、B两点，求△ABF2的面积．
查看答案
考题 顶点在原点、焦点在χ轴上且通径(过焦点和对称轴垂直的弦)长为6的抛物线方程为_____．
查看答案
考题 抛物线y2＝4x上一点P到焦点F的距离是10，则点P坐标是（　　）A.(9，6) B.(9，±6) C.(6，9) D.(±6，9)
查看答案
考题 以抛物线y2＝8x的焦点为圆心，且与此抛物线的准线相切的圆的方程是（　　）A.(x＋2)2＋y2＝16 B.(x＋2)2＋y2＝4 C.(x－2)2＋y2＝16 D.(x－2)2＋y2＝4
查看答案
考题 设直线y=2x+m与抛物线y2=4x没有公共点，则m的取值范围是。
查看答案
考题 A．B是抛物线y2=8x上两点，且此抛物线的焦点在线段AB上，已知A．B两点的横坐标之和为10，则|AB|=（　　）A.18 B.14 C.12 D.10
查看答案
考题 设曲线y=y（x）过（0，0）点，M是曲线上任意一点，MP是法线段，P点在x轴上，已知MP的中点在抛物线，求此曲线的方程。
查看答案
考题 求过点A(1，-2)的所有直线被圆x2+y2=5截得线段中点的轨迹方程。
查看答案
考题 椭圆的焦点分别是F1和F2，已知椭圆的离心率 ．过中心O 作直线与椭圆交于A，B两点，O为原点，若△ABF2的面积是20。 (1)求m的值； (2)直线AB的方程。
查看答案
考题 点在平面内的运动方程为，则其轨迹为（ ）。 A.椭圆曲线 B.圆弧曲线 C.直线 D.抛物线
查看答案
考题 已知M是抛物线y2=2px(p>0)上的点，F是抛物线的焦点，∠FOM=45o，|MF|=2。 (1)求抛物线的方程式；
查看答案
考题 已知P为抛物线y2=x的焦点，点M，N在该抛物线上且位于x轴的两侧， (其中O为坐标原点)，则ΔMPO与ΔNPO面积之和的最小值是( )。
查看答案
考题 设抛物线y2=2px(p>0)焦点为F，点A坐标为(0，2)，若线段FA的中点B在抛物线上，则B到该抛物线准线距离为__________。
查看答案
考题 过抛物线y2=4x的焦点，倾斜角为45°的直线方程为_______。
查看答案
考题 已知抛物线y2=2px(p>0)，过定点(p，0)作两条互相垂直的直线l1、l2，l1与抛物线交于
查看答案
考题 曲线方程y2=2px所描述的是（）。A、摆线B、渐开线C、双曲线D、抛物线
查看答案
考题 方程 y2 = 2px（p＞0）是抛物线标准方程（SIEMENS系统）。
查看答案
考题 方程y2=2px（p＞0）是抛物线标准方程（FANUC系统、华中系统）。
查看答案
考题 假定导线的荷载，视为沿直线均匀分布推出的公式称为（）。A、平抛物线方程B、斜抛物线方程C、悬链线方程D、状态方程
查看答案
考题 填空题若直线ax－y＋1＝0经过抛物线y2＝4x的焦点，则实数a＝____．
查看答案
考题 单选题过抛物线y＝4x的焦点，作直线与此抛物线相交于两点P和Q，那么线段PQ中点的轨迹方程（）A y＝2x－1B y＝2x－2C y＝－2x＋1D －2x＋2
查看答案
热门标签
最新试卷