网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
函数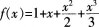 的图象与x轴交点的个数是( )。
的图象与x轴交点的个数是( )。
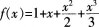 的图象与x轴交点的个数是( )。
的图象与x轴交点的个数是( )。A、0
B、1
C、2
D、3
B、1
C、2
D、3
参考答案
参考解析
解析: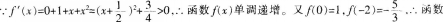 f(x)的图象与x轴有且只有一个交点。故选B。
f(x)的图象与x轴有且只有一个交点。故选B。
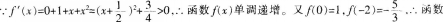 f(x)的图象与x轴有且只有一个交点。故选B。
f(x)的图象与x轴有且只有一个交点。故选B。
更多 “函数的图象与x轴交点的个数是( )。A、0 B、1 C、2 D、3 ” 相关考题
考题
作出函数y=3-2x的图象,根据图象回答下列问题:(1)y的值随着x值增大而__________;(2)图象与x轴的交点坐标是_________________,与y轴的交点坐标是_______________;(3)当x__________时,y>0 。
考题
在同一直角坐标系内一次作出函数y=x+1,y=2x+1,y=3x+1的图象。(1)这几个图象之间有什么差别,又有什么联系?(2)一次函数y=kx+b的一次项系数k对函数的图象有什么影响?
考题
已知一次函数的图象经过点A(2,1),B(-1,-3)(1)求此一次函数的解析式;(2)求此一次函数的图象与x轴、y轴的交点坐标;(3)求此一次函数的图象与两坐标轴所围成的三角形面积。
考题
A.常数k<-1
B.函数f(x)在定义域范围内,y随着x的增大而减小
C.若点C(-1,m),点B(2,n),在函数f(x)的图象上,则m<n
D.函数f(x)图象对称轴的直线方程是y=x
考题
函数f(x)=2sin3x的图象按向量a平移后得到的图象与g(x)=2cos3x的图象重合,则向量a可以是A.(-π/2,0)
B.(π/2,0)
C.(-π/6,0)
D.(π/6,0)
考题
下图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4).
(1)求出图象与戈轴的交点A,B的坐标;
存在,请说明理由;
° (3)将二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线y=x+b(b<1)与此图象有两个公共点时,b的取值范围.
考题
已知曲线,其中函数f(t)具有连续导数,且f(0)=0,f'(t)>0(0).若曲线L的切线与x轴的交点到切点的距离恒为1,求函数f(t)的表达式,并求以曲线L及x轴和y轴为边界的区域的面积.
考题
设χ=α是代数方程f(χ)=0的根,则下列结论不正确的是( )。
A、χ-α是f(χ)的因式
B、χ-α整除f(χ)
C、(α,0)是函数y=f(χ)的图象与χ轴的交点
D、f′(α)=O
考题
案例:
某教师关于“反比例函数图象”教学过程中的三个步骤为:
第一步:复习回顾
提出问题:我们已经学过一次函数的哪些内容 是如何研究的
第二步:引入新课。
提出问题:反比例函数的图象是什么形状呢
引导学生利用描点法画出y=1/2的图象。
列表:
描点:
连线:引导学生用光滑的曲线连接描点,并用计算机演示图象的生成过程。在此过程中启发学生思考,由于X,Y都不能为0,所以函数图象与X轴、Y轴不能有交点(如下图)
……(第三步过程省略)
(1)该教学过程的主要特点是什么 (8分)
(2)在第二步的连线过程中,如果你是该老师,如何引导学生思考所连的线不是直线,而是光滑曲线(6分)
(3)对于第三步的③,如果你是该老师,如何引导学生思考函数图象在第一象限(或第三象限)的变化 (6分)
考题
设x=a是代数方程f(x)=0的根,则下列结论不正确的是( )。
A、 叫是f(x)的因式
B、X-a整除f(x)
C、(a,0)是函数y=f(x)的图象与2轴的交点
D、 f(a)=0
考题
某教师关于“反比例函数图象”教学过程中的三个步骤为:
第一步:复习回顾
提出问题:我们已经学过一次函数的哪些内容?是如何研究的?
第二步:引入新课。
提出问题:反比例函数的图形是什么形状呢?
引导学生利用描点法画出y=1/x的图象。
列表:
描点:
连线:引导学生用光滑的曲线连接描点,并用计算机演示图象的生成过程。在此过程中启发学生思考,由于x,y都不能为0,所以函数图象与x轴、y轴不能有交点(如下图)
……(第三步过程省略)
(1)该教学过程的主要特点是什么?
(2)在第二步的连线过程中,如果你是该老师,如何引导学生思考所连的线不是直线,而是光滑曲线
(3)对于第三步的③,如果你是该老师,如何引导学生思考函数图象在第一象限(或第三象限)的变化?
考题
用简单迭代法求方程f(x)=0的实根,把方程f(x)=0表示成x=φ(x),则f(x)=0的根是()。A、y=φ(x)与x轴交点的横坐标B、y=x与y=φ(x)交点的横坐标C、y=x与x轴的交点的横坐标D、y=x与y=φ(x)的交点
考题
单选题如果a,b,c成等比数列,那么函数f(x)=ax2+bx+c的图像与x轴的交点个数是( ).A
0个B
恰有一个C
2个D
不能确定
热门标签
最新试卷