网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
举例说明向量内容的学习对高中生理解数学运算的作用。
参考答案
参考解析
解析:本题主要考查高中数学课程内容的基础知识以及立体向量的基本性质。
运算是数学学习的一个基本内容。运算对象的不断扩展是数学法则的一条重要线索。从数的运算到字母的运算,是运算的一次跳跃。数的运算可以用来刻画具体问题中的数量关系,解决一个一个有关数量的具体问题,而字母运算则可以刻画蕴涵规律的一类问题。从数的运算,到向量的运算是认识运算的又一次跳跃。而向量运算更加清晰地展示了“
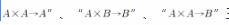
三种类型的代数运算的特征以及代数运算的功能,这对于学生进一步学习其他数学运算、增强学生的运算能力具有基础作用。
运算是数学学习的一个基本内容。运算对象的不断扩展是数学法则的一条重要线索。从数的运算到字母的运算,是运算的一次跳跃。数的运算可以用来刻画具体问题中的数量关系,解决一个一个有关数量的具体问题,而字母运算则可以刻画蕴涵规律的一类问题。从数的运算,到向量的运算是认识运算的又一次跳跃。而向量运算更加清晰地展示了“
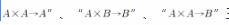
三种类型的代数运算的特征以及代数运算的功能,这对于学生进一步学习其他数学运算、增强学生的运算能力具有基础作用。
更多 “举例说明向量内容的学习对高中生理解数学运算的作用。” 相关考题
考题
小学数学运算规则学习内容特点包括()
A、以认数学习为起点B、以整数四则运算为主线C、小数与分数的性质和运算规则学习与认数学习交织进行的D、运算技巧是运算规则学习的重点E、性质与概念学习是伴随着运算规则学习而展开的
考题
建构小学数学课堂教学策略的依据主要包括()。
A、对学生学习数学成绩的要求B、对小学数学教育价值追求的基本认识C、对儿童学习数学过程的认识和理解D、对课堂学习过程的理解和诠释E、对教师自身价值的认识
考题
高中数学《空间向量》
二、考题解析
【教学过程】
(一)引入课题
(课件)引入:有一块质地均匀的正三角形面的钢板,重500千克,顶点处用与对边成60度角,大小200千克的三个力去拉三角形钢板,问钢板在这些力的作用下将如何运动?这三个力至少多大时,才能提起这块钢板?
提问:我们研究的问题是三个力的问题,力在数学中可以看成是什么?这三个向量和以前我们学过的向量有什么不同?
(学生得出:这是三个向量不共面)
追问:不共面的向量问题能直接用平面向量来解决么?解决这类问题需要空间向量的知识。这节课我们就来学习空间向量。
(二)探求新知
1.生活实例感知
空间向量我们随处可见,同学们能不能举出一些例子?(学生举例)
再演示(课件)几种常见的空间向量身影。(常见的高压电线及支架所在向量,长方体中的三个不共线的边上的向量,平行六面体中的不共线向量)
2.类比概念形成
接下来我们我们就来研究空间向量的知识、概念和特点,空间向量与平面向量既有联系又有区别,我们将通过类比的方法来研究空间向量,首先我们复习回顾一下平面向量的知识。师生一起回忆平面向量概念、向量的模、零向量、单位向量、相反向量、相等向量等,引导学生理解空间向量就是把向量放到空间中了,请同学们给空间向量下个定义,
(学生:在空间中,既有大小又有方向的量)
现在请同学们阅读教材,找出空间向量的相关定义,用类比的方法记忆并填写课件的表格:
3.类比运算定律形成
在数学中引入一种量以后,一个很自然的问题就是研究它们的运算,空间向量的运算我们也采用与平面向量类比的方法,那么我们首先来复习回顾一下平面向量的加减运算。(课件)复习回顾:(找学生回答)
提问:同学课下的复习很好。我们先来探讨这样一个问题:对于两个向量来说空间向量和平面向量有没有区别?
学生探讨研究:平面向量可在同一平面内平移,而空间向量也可在空间中平移。平移后的向量与原向量是同一向量。由此得出:空间任意两个向量都可转化为共面向量。
引导学生得出任意的空间中的两个向量的运算与平面向量的结论一致,这样我们就能够定义空间向量的加法和减法运算。
同样地,用类比(表格)形式对比给出空间向量的相关定义,采用填空形式填写下列有关内容:(课件)
(三)巩固提高
课堂练习例1.
(四)小结作业
这节课,我们在平面向量的基础上学习了平面向量,接下来给同学们两分钟的时间总结一下这节课的主要内容。(学生总结)
通过这节课的学习,我们学会了空间向量的有关概念,加减运算及其运算律以及空间向量的加减运算在空间几何体中的应用。
作业:(1)课后练习题1、2;
(2)思考题:共始点的两个不共线向量的加法满足平行四边形法则。和向量是平行四边形的对角线。请问,共始点的三个不共面的向量满足什么法则?和向量是什么向量?
【板书设计】
【答辩题目解析】
1.平行向量是如何定义的?
2.空间向量在高中数学中具有怎样的地位和作用?
考题
《普通高中数学课程标准(实验)》指出:“学生对基础知识和基本技能的理解与掌握是数学教学的基本要求,也是评价学生学习的基本内容;评价要注重对数学本质的理解和思想方法的把握,避免片面强调机械记忆,模仿以及复杂技巧。”请分别给出评价学生基础知识与基本技能掌握情况的具体建议,并举例说明。
考题
下列对向量学习意义的描述:
①有助于学生体会数学与现实生活和其他学科的联系;?
②有助于理解数学运算的意义和价值,发展运算能力;?
③有助于掌握处理,几何问题的一种方法,体会数形结合思想;?
④有助于理解数学不同内容之间存在广泛的联系.?
其中正确的共有( ).A.1条
B.2条
C.3条
D.4条
考题
在学习“平面向量”后,某数学教师安排了如下一道选择题:
以下是三位学生的解法:
问题:
(1)如果你是这位数学教师,请指出这三种解法存在的错误;(9分)
(2)请你从已知条件|
出发,通过数形结合,引导学生给出一种正确的解法;(5分)
(3)针对学生在向量运算中的错误,请写出实数运算与向量运算的不同点(至少写出三点)。(6分)
考题
向量是近代数学中重要和基本的数学概念之一,下面是高中必修课程数学4“平面向量”第二章第一节“平面向量的实际背景及基本概念”的部分教材内容。
阅读教材,回答下列问题:
(1)谈谈“向量”在高中数学课程中的作用;
(2)分析上面教材的设计思路
(3)确定“平面向量概念”教学目标和教学重难点;
(4)根据教材,设计一个“平面向量概念”引入的教学片段要求;引导学生从实际背景抽象概念的过程。
考题
单选题“按照儿童智慧运算结构形成的特点和规律组织数学教育的内容”是肖湘宁在( )中提出的。A
《学前儿童数学教育》B
《入学前数学教育》C
《幼儿数学活动教学法》D
《儿童怎样学习数学》
考题
问答题请举例说明小学数学运算规则学习的特点。
热门标签
最新试卷