网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设函数z=f(xy,yg(x)),其中函数f具有二阶连续偏导数,函数g(x)可导且在x=1处取得极值g(1)=1.求

参考答案
参考解析
解析: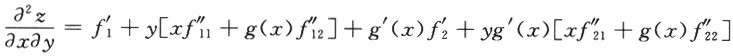
所以,令x=y=1,且注意到g(1)=1,g'(1)=0,得

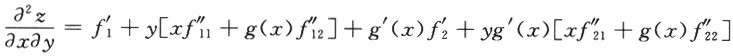
所以,令x=y=1,且注意到g(1)=1,g'(1)=0,得

更多 “设函数z=f(xy,yg(x)),其中函数f具有二阶连续偏导数,函数g(x)可导且在x=1处取得极值g(1)=1.求” 相关考题
考题
以下结论正确的是()。
A、若x0为函数y=f(x)的驻点,则x0必为函数y=f(x)的极值点.B、函数y=f(x)导数不存在的点,一定不是函数y=f(x)的极值点.C、若函数y=f(x)在x0处取得极值,且f′(x)存在,则必有f′(x)=0.D、若函数y=f(x)在x0处连续,则y=f′(x0)一定存在.
考题
函数厂(x)具有连续的二阶导数,且f″(0)≠0,则x=0( )。A.不是函数f(x)的驻点
B.一定是函数f(x)的极值点
C.一定不是函数f(x)的极值点
D.是否为函数f(x)的极值点,还不能确定
考题
A.只能确定一个具有连续偏导数的隐函数z=z(x,y)
B.可确定两个具有连续偏导数的隐函数y=y(x,y)和z=z(x,y)
C.可确定两个具有连续偏导数的隐函数x=x(x,y)和z=z(x,y)
D.可确定两个具有连续偏导数的隐函数x=x(y,z)和y=y(x,z)
考题
设有三元方程 ,根据隐函数存在定理,存在点(0,1,1)的一个邻域,在此邻域内该方程A.只能确定一个具有连续偏导数的隐函数z=z(x,y)
B.可确定两个具有连续偏导数的隐函数x=x(y,z)和z=z(x,y)
C.可确定两个具有连续偏导数的隐函数y=y(x,z)和z=z(x,y)
D.可确定两个具有连续偏导数的隐函数x=x(y,z)和y=y(x,z)
考题
设函数f(x)具有二阶导数,g(x)=f(0)(1-x)+f(1)x,则在区间[0,1]上
A.A当f'(x)≥0时,f(x)≥g(x)
B.当f'(x)≥0时,f(x)≤g(x)
C.当f"(x)≥0时,f(x)≥g(x)
D.当f"(x)≥0时,f(x)≤g(x)
考题
设函数f(x)具有二阶连续导数,且f(x)>0,f'(0)=0,则函数z=f(x)lnf(y)在点(0,0)处取得极小值的一个充分条件是
A.Af(0)>1,f"(0)>0
B.f(0)>1,f"(0)C.f(0)0
D.f(0)
考题
下列命题中,正确的是( ).A.单调函数的导函数必定为单调函数
B.设f(x)为单调函数,则f(x)也为单调函数
C.设f(x)在(a,b)内只有一个驻点xo,则此xo必为f(x)的极值点
D.设f(x)在(a,b)内可导且只有一个极值点xo,f(xo)=0
考题
设函数f(x),g(x)是大于零的可导函数,且f′(x)g(x)-f(x)g′(x)<0,则当a<x<b时有( )《》( )A.f(x)g(b)>f(b)g(x)
B.f(x)g(a)>f(a)g(x)
C.f(x)g(x)>f(b)g(b)
D.f(x)g(x)>f(a)g(a)
考题
问答题设函数f(x),g(x)在[a,b]上连续,在(a,b)内二阶可导,且存在相等的最大值。若f(a)=g(a),f(b)=g(b),证明: (1)存在η∈(a,b)使f(η)=g(η); (2)存在ξ∈(a,b)使f″(ξ)=g″(ξ)。
考题
单选题设三元函数xy-zlny+exz=1,根据隐函数存在定理,存在点(0,1,1)的一个邻域,在此邻域内该方程( )。A
只能确定一个具有连续偏导数的隐函数z=z(x,y)B
可确定两个具有连续偏导数的隐函数y=y(x,z)和z=z(x,y)C
可确定两个具有连续偏导数的隐函数x=x(y,z)和z=z(x,y)D
可确定两个具有连续偏导数的隐函数x=x(y,z)和y=y(x,z)
考题
问答题设函数f(x),g(x)二次可导,满足函数方程f(x)g(x)=1,又f′(x)≠0,g′(x)≠0,则f″(x)/f′(x)-f′(x)/f(x)=g″(x)/g′(x)-g′(x)/g(x)。
热门标签
最新试卷