网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设函数f(x)与g(x)在[0,1]上连续,且f(x)≤g(x),且对任何的c∈(0,1)( )
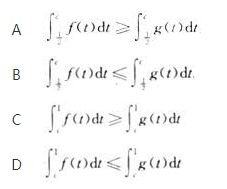
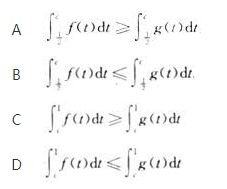
参考答案
参考解析
解析: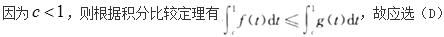
更多 “设函数f(x)与g(x)在[0,1]上连续,且f(x)≤g(x),且对任何的c∈(0,1)( ) ” 相关考题
考题
若函数y=f(x)是一随机变量的概率密度,则()一定成立。
A、y=f(x)的定义域为[0,1]B、y=f(x)非负C、y=f(x)的值域为[0,1]D、y=f(x)在(-∞,+∞)内连续
考题
设f(x)、g(x)在区间[a,b]上连续,且g(x)<f(x)<m(m为常数),由曲线y=g(x),y=f(x),x=a及x=b所围平面图形绕直线y=m旋转而成的旋转体体积为( )。A.
B.
C.
D.
考题
以下四个命题中,正确的是( )A.f′(x)在(0,1)内连续,则f′(x)在(0,1)内有界
B.f(x)在(0,1)内连续,则f(x)在(0,1)内有界
C.f′(x)在(0,1)内连续,则f(x)在(0,1)内有界
D.f(x)在(0,1)内连续,则f′(x)在(0,1)内有界
考题
设函数f(x),g(x)在[a,b]上均可导(a<b),且恒正,若f′(x)g(x)+f(x)g′(x)>0,则当x∈(a,b)时,下列不等式中成立的是( )。
A. [f(x)/g(x)]>[f(a)/g(b)]
B. [f(x)/g(x)]>[f(b)/g(b)]
C. f(x)g(x)>f(a)g(a)
D. f(x)g(x)>f(b)g(b)
考题
设函数f(x)具有二阶导数,g(x)=f(0)(1-x)+f(1)x,则在区间[0,1]上
A.A当f'(x)≥0时,f(x)≥g(x)
B.当f'(x)≥0时,f(x)≤g(x)
C.当f"(x)≥0时,f(x)≥g(x)
D.当f"(x)≥0时,f(x)≤g(x)
考题
设函数f(x),g(x)是大于零的可导函数,且f′(x)g(x)-f(x)g′(x)<0,则当a<x<b时有( )《》( )A.f(x)g(b)>f(b)g(x)
B.f(x)g(a)>f(a)g(x)
C.f(x)g(x)>f(b)g(b)
D.f(x)g(x)>f(a)g(a)
考题
已知函数
(1)求f(x)单调区间与值域;
(2)设a≥1,函数g(x)=x3-3a2x-2a,x∈[0,1]。若对于任意x1∈[0,1],总存在x0∈[0,1]使g(x0)=f(x1)成立,求a的取值范围。
考题
设g(x),f(x)∈F[x],存在d(x)∈F[x],有d(x)|f(x)且d(x)|g(x),那么称d(x)为f(x),g(x)的什么?()A、公因式B、最大公因式C、最小公因式D、共用函数
考题
问答题设函数f(x)在闭区间[0,1]上可微,对于[0,1]上的每一个x,函数f(x)的值都在开区间(0,1)内,且f′(x)≠1,证明在(0,1)内有且仅有一个x,使得f(x)=x。
考题
问答题设f(x)在[0,1]上具有二阶导数,且满足条件|f(x)|≤a,|f″(x)|≤b(其中a、b都是非负常数),c是(0,1)内任一点。 (1)写出f(x)在点x=c处带拉格朗日余项的一阶泰勒公式; (2)证明:|f′(c)|<2a+b/2。
考题
单选题设g(x),f(x)∈F[x],存在d(x)∈F[x],有d(x)|f(x)且d(x)|g(x),那么称d(x)为f(x),g(x)的什么?()A
公因式B
最大公因式C
最小公因式D
共用函数
考题
问答题设函数f(x),g(x)在[a,b]上连续,在(a,b)内二阶可导,且存在相等的最大值。若f(a)=g(a),f(b)=g(b),证明: (1)存在η∈(a,b)使f(η)=g(η); (2)存在ξ∈(a,b)使f″(ξ)=g″(ξ)。
考题
单选题设函数f(x),g(x)在[a,b]上均可导(a<b),且恒正,若f′(x)g(x)+f(x)g′(x)>0,则当x∈(a,b)时,下列不等式中成立的是( )。[2018年真题]A
f(x)/g(x)>f(a)/g(b)B
f(x)/g(x)>f(b)/g(b)C
f(x)g(x)>f(a)g(a)D
f(x)g(x)>f(b)g(b)
考题
问答题设函数f(x),g(x)在[a,b]上连续,在(a,b)内可导,且对于(a,b)内一切x有f′(x)g(x)-f(x)g′(x)≠0。证明:如果f(x)在(a,b)内有两个零点,则介于两个零点之间,g(x)至少有一个零点。
热门标签
最新试卷