考题
求解线性方程组最基本的一种直接法是追赶法。()
考题
通常把按照先消元、后回代两个步骤求解线性方程组的方法称为高斯(Gauss)消去法。()
考题
阐述矩阵乘法的运算过程。并用矩阵乘积形式表示如下线性方程组。
用初等变换的方法求解上述线性方程组。
考题
设β1,β2是线性方程组Ax=b的两个不同的解,α1、α2是导出组Ax=0的基础解系,k1,k2是任意常数,则Ax=b的通解是:
考题
设β1,β2是线性方程组Ax=b的两个不同的解,a1,a2是导出组Ax=0的基础解系,k1、k2是任意常数,则Ax=b的通解是:
考题
已知是线性方程组的解, 是它的导出组的解,求方程组的通解。
考题
设齐次线性方程组其中ab≠0,n≥2.讨论a,b取何值时,方程组只有零解、有无穷多个解?在有无穷多个解时求出其通解.
考题
参数a取何值时,线性方程组有无数个解?并求其通解.
考题
已知3阶矩阵A的第一行是不全为零,矩阵 (k为常数),且AB=0, 求线性方程组Ax=0的通解
考题
取何值时,非齐次线性方程组 (1)有唯一解 (2)无解 (3)有无穷多个解? 并在无穷多个解时,求方程组的通解。
考题
设有下列线性方程组(Ⅰ)和(Ⅱ) (Ⅰ) (Ⅱ) (1) 求方程组(Ⅰ)的通解; (2) 当方程组(Ⅱ)中的参数m,n,t为何值时,(Ⅰ)与(Ⅱ)同解?
考题
已知非齐次线性方程组 有3个线性无关的解. (Ⅰ)证明方程组系数矩阵A的秩; (Ⅱ)求的值及方程组的通解
考题
设有齐次线性方程组
试问a为何值时,该方程组有非零解,并求其通解.
考题
问取何值时 非齐次线性方程组, (1)有唯一解 (2)无解 (3)有无穷多个解,并在无穷多个解时,求方程组的通解
考题
已知下列非齐次线性方程组(Ⅰ),(Ⅱ)
(1)求解方程组(Ⅰ),用其导出组的基础解系表示通解.
(2)当方程组中的参数m,n,t为何值时,方程组(Ⅰ)与(Ⅱ)同解.
考题
设有齐次线性方程组.试问取何值时,该方程组有非零解,并求出其通解
考题
讨论a、b为何值时非齐次线性方程组有无穷多解,并求其通解。
考题
设A=(α1,α2,α3)为3阶矩阵.若α1,α2线性无关,且α3=-α1+2α1,则线性方程组Ax=0的通解为________.
考题
设,.
已知线性方程组Ax=b存在2个不同的解.
(Ⅰ)求λ,a;
(Ⅱ)求方程组Ax=b的通解.
考题
(1)求|A|;
(2)已知线性方程组AX=b有无穷多解,求a,并求A=b的通解。
考题
设(1)求lAl;
(2)已知线性方程组AX-b有无穷多解,求a,并求AX=b的通解。
考题
通过对有限元的态体分析,目的是要建立一个()来揭示结点外载荷与结点位移的关系,从而用来求解结点位移。A、变换矩阵B、非线性方程组C、线性方程组D、目标函数
考题
填空题对于线性方程组Ax=B,其求解方式为()。
考题
填空题设n阶矩阵A的各行元素之和均为零,且A的秩为n-1,则线性方程组AX=O的通解为____.
考题
单选题通过对有限元的态体分析,目的是要建立一个()来揭示结点外载荷与结点位移的关系,从而用来求解结点位移。A
变换矩阵B
非线性方程组C
线性方程组D
目标函数
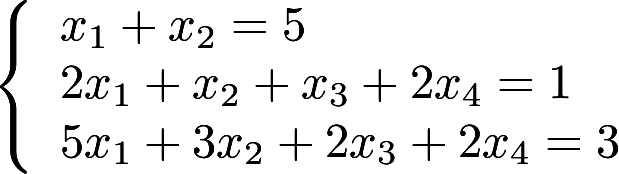 的通解。
的通解。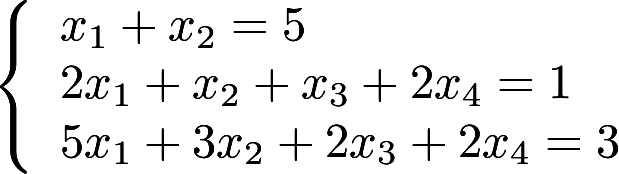 的通解。
的通解。
