网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设A和B都是n阶矩阵.记,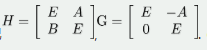 . (1)求HG和GH. (2)证明|E-AB|=|E-BA|.
. (1)求HG和GH. (2)证明|E-AB|=|E-BA|.
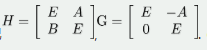 . (1)求HG和GH. (2)证明|E-AB|=|E-BA|.
. (1)求HG和GH. (2)证明|E-AB|=|E-BA|.参考答案
参考解析
解析:

更多 “设A和B都是n阶矩阵.记,. (1)求HG和GH. (2)证明|E-AB|=|E-BA|.” 相关考题
考题
填空题设A为n阶方阵,E为n阶单位矩阵,且A2=A,则(A-2E)-1=____。
热门标签
最新试卷