网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
曲线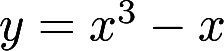 与其在
与其在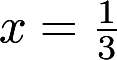 处的切线所围成的部分被y轴分成两部分, 这两部分面积之比是
处的切线所围成的部分被y轴分成两部分, 这两部分面积之比是
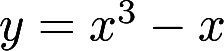 与其在
与其在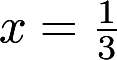 处的切线所围成的部分被y轴分成两部分, 这两部分面积之比是
处的切线所围成的部分被y轴分成两部分, 这两部分面积之比是参考答案
参考解析
解析:

更多 “曲线 与其在 处的切线所围成的部分被y轴分成两部分, 这两部分面积之比是” 相关考题
考题
设函数f(x)在定义域I上的导数大于零,若对任意的x0∈I,曲线y=f(x)在点(x0,f(x0))处的切线与直线x=x0及x轴所围成区域的面积恒为4,且f(0)=2,求f(x)的表达式.
考题
单选题曲线y-=cosx在[0,2π]上与x轴所围成图形的面积是:()A
0B
4C
2D
1
热门标签
最新试卷