网友您好， 请在下方输入框内输入要搜索的题目：
题目内容
（请给出正确答案）
总体X～N(μ,5^2),则总体参数μ的置信度为1－a的置信区间的长度().
A.与α无关
B.随α的增加而增加
C.随α的增大而减少
D.与α有关但与α的增减性无关
B.随α的增加而增加
C.随α的增大而减少
D.与α有关但与α的增减性无关
参考答案
参考解析
解析：总体方差已知，参数卢的置信度为1-α的置信区间为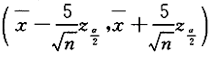
，其中n为样本容量，长度
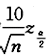，因为α越小，则
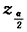越大，所以置信区间的长度随α增大而减少，选(C).
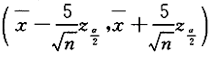，其中n为样本容量，长度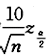，因为α越小，则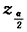越大，所以置信区间的长度随α增大而减少，选(C).
更多 “总体X～N(μ,5^2),则总体参数μ的置信度为1－a的置信区间的长度().A.与α无关 B.随α的增加而增加 C.随α的增大而减少 D.与α有关但与α的增减性无关” 相关考题
考题
设某厂生产电阻器的阻值X～N(60.5，1.22)，已知该厂电阻器阻值的规范界限为60±2，则超过上限的概率可表示为( )。. 设X～N(μ，σ2)，σ未知，从中抽取n＝16的样本，其样本均值为x，样本标准差为s，则总体均值μ的置信度为95%的置信区间为( )。A． [*]
考题
从一个服从正态分布的总体中随机抽取样本容量为n的样本，在95%的置信度下对总体参数进行估计的结果为：20±0.08。如果其他条件不变，样本量扩大到原来的4倍，则总体参数的置信区间应该是（ ）。A.20±0.16B.20±0.04C.80±0.16D.80±0.04
考题
设θ是总体的一个待估参数，现从总体中抽取容量为n的一个样本，从中得到参数θ的一个置A.B.100个置信区间中约有90个区间能包含真值θC.100个置信区间中约有5个区间能包含真值0D.E.100个置信区间中约有90个区间不能包含真值θ
考题
θ是总体的一个待估参数，θL,θU是其对于给定a的1-a的置信下限与置信上限。则1-a置信区间的含义是（ ）。
A.所构造的随机区间[θL,θU]覆盖（盖住）未知参数θ的概率为1 - a
B.由于这个随机区间随样本观测值的不同而不同，它有时覆盖住了参数θ，有时则没有覆盖参数θ
C.用这种方法做区间估计时，不能覆盖参数θ的机率相当小
D.如果P(θL) =P(θ>θU)=a/2，则称这种置信区间为等尾置信区间
E.正态总体参数的置信区间是等尾置信区间，而比例p的置信区间不是等尾置信区间
考题
设总体X～N(u，σ2），基于来自总体X的容量为16的简单随机样本，测得样本均值x= 31.645，样本方差S2=0.09，则总体均值μ的置信度为0.98的置信区间为( )。
A.(30.88, 32.63)
B.(31.45, 31.84)
C.(31.62, 31.97)
D.(30.45, 31.74)
考题
从一个服从正态分布的总体中随机抽取样本容量为n的样本，在95％的置信度下对总体参数进行估计的结果为20±0．08。如果其他条件不变，样本容量扩大到原来的4倍，则总体参数的置信区间应该是（）。A.20±0．16
B.20±0．04
C.80±0．16
D.80±0．04
考题
设总体X～N(u，σ2），基于来自总体X的容量为16的简单随机样本，测得样本均值图.png= 31.645，样本方差S2=0.09，则总体均值μ的置信度为0.98的置信区间为()。
A.(30.88, 32.63)
B.(31.45, 31.84)
C.(31.62, 31.97)
D.(30.45, 31.74)
考题
设总体X～N（μ，σ2），其中σ2未知，则总体均值μ的置信区间长度L与1-α的关系是（）。A、当1-α缩小时，L缩短B、当1-α缩小时，L增大C、当1-α缩小时，L不变D、以上说法都不变
考题
设x1，…，X是取自总体X的容量为n的样本．已知总体X服从参数为p的二点分布，则等于（）．A、np（p）B、（n-1）p（p）C、npD、np2
热门标签
最新试卷