网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
如果f(x)=e-x,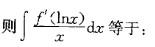
A. -1/x+c
B. 1/x+c
C. -lnx+c
D. lnx+c
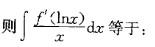
A. -1/x+c
B. 1/x+c
C. -lnx+c
D. lnx+c
参考答案
参考解析
解析:提示:用凑微分法把式子写成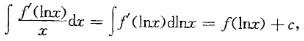 再把lnx代入
再把lnx代入
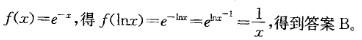
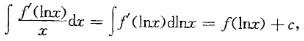 再把lnx代入
再把lnx代入
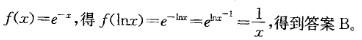
更多 “如果f(x)=e-x, A. -1/x+c B. 1/x+c C. -lnx+c D. lnx+c” 相关考题
考题
方程y"-2y'+5y=0的通解为( )。A y=ex(c1cosx+c2sinx)
B y=e-x(c1cos2x+c2sin2x)
C y=ex(c1cos2x+c2sin2x)
D y=e-x(c1cosx+c2sinx)
考题
如果∫df(x)=∫dg(x),则下列各式中哪一个不一定成立?
A.f(x)=g(x)
B.f'(x)=g'(x)
C.df(x)=dg(x)
D.d∫f'(x)dx=d∫g'(x)dx
考题
设连续型随机变量X的密度函数为f(x),分布函数为F(x).如果随机变量X与-X分布函数相同,则().
A.F(z)=F(-x)
B.F(x)=F(-x)
C.F(X)=F(-x)
D.f(x)=f(-x)
考题
单选题如果二阶常系数非齐次线性微分方程y″+ay′+by=e-xcosx有一个特解y*=e-x(xcosx+xsinx),则( )。A
a=-1,b=1B
a=1,b=-1C
a=2,b=1D
a=2,b=2
考题
单选题微分方程y″-2y′+y=0的两个线性无关的特解是( )。[2016年真题]A
y1=x,y2=exB
y1=e-x,y2=exC
y1=e-x,y2=xe-xD
y1=ex,y2=xex
考题
单选题设F(x)是f(x)的一个原函数,则等于()。A
F(e-x)+CB
-F(e-x)+CC
F(ex)+CD
-F(ex)+C
热门标签
最新试卷