网友您好， 请在下方输入框内输入要搜索的题目：
题目内容
（请给出正确答案）
y″+5y′=0的特征方程为——．
参考答案
参考解析
解析：由特征方程的定义可知，所给方程的特征方程为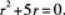
【评析】如果是求该方程的解，则可以将所给方程作为可降阶方程求解，但当作二阶线性常系数方程求解较简便．
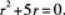【评析】如果是求该方程的解，则可以将所给方程作为可降阶方程求解，但当作二阶线性常系数方程求解较简便．
更多 “y″+5y′=0的特征方程为——．” 相关考题
考题
下列程序段的执行结果为______。X=5Y=-20If Not X＞0 Then X=Y-3 Else Y=X+3Print X-Y；Y-XA．-3 3B．5 -8C．3 -3D．25 -25
考题
方程y"-2y'+5y=0的通解为( )。A y=ex(c1cosx+c2sinx)
B y=e-x(c1cos2x+c2sin2x)
C y=ex(c1cos2x+c2sin2x)
D y=e-x(c1cosx+c2sinx)
考题
已知r1=3，r2=-3是方程y"+py'+qy=0（p和q是常数）的特征方程的两个根，则该微分方程是下列中哪个方程？
A. y"+9y'=0
B. y"-9y'=0
C. y"+9y=0
D. y"-9y=0
考题
若二阶常系数线性齐次微分方程y"+ay'+by=0的通解为y=(C1+C2x)e^x，则非齐次方程y"+ay'+by=x满足条件y(0)=2，y'(0)=0的解为y=________.
考题
已知。r1=3,r2=-3是方程y+py+q=0 (p和q是常数）的特征方程的两个根, 则该微分方程是（ ）。
A. y+9y=0= 0 B. y-9y=0
C. y+9y=0 D.y-9y=0=0
考题
单选题以y1＝ex，y2＝e2xcosx为特解的最低阶数的常系数线性齐次方程为（ ）。A
y‴－5y″－9y′－5y＝0B
y‴－5y″－5y′－5y＝0C
y‴－5y″＋9y′－5y＝0D
y‴－5y″＋5y′－5y＝0
考题
单选题微分方程y″－4y′＋5y＝0的通解为（ ）。A
ex（C1cos2x＋C2sin2x）B
C1e－x＋C2e5xC
e2x（C1cosx＋C2sinx）D
C1ex＋Ce－5x
考题
单选题以y1＝ex，y2＝e2xcosx为特解的最低阶数的常系数线性齐次方程为（ ）。A
y‴＋5y″＋9y′＋5y＝0B
y‴＋5y″＋9y′－5y＝0C
y‴－5y″＋9y′＋5y＝0D
y‴－5y″＋9y′－5y＝0
考题
单选题已知r1=3，r2=-3是方程y″+Py′+qy=0（p和q是常数）的特征方程的两个根，则该微分方程是下列中哪个方程？（）A
y″+9y′=0B
y″-9y′=0C
y″+9y=0D
y″-9y=0
考题
单选题曲线y＝y（x）经过原点且在原点处的切线与直线2x＋y＝6平行，而y＝y（x）满足方程y″－2y′＋5y＝0，则此曲线的方程为（ ）。A
y＝exsin2xB
y＝－exsin2xC
y＝exsinxD
y＝－exsinx
考题
单选题若曲线C上点的坐标都是方程f（x，y）＝0的解，则下列判断中正确的是（ ）．A
曲线C的方程是f（x，y）＝0B
以方程f（x，y）＝0的解为坐标的点都在曲线C上C
方程f（x，y）＝0的曲线是CD
方程f（x，y）＝0表示的曲线不一定是C
考题
单选题曲线y＝y（x）经过原点且在原点处的切线与直线2x＋y＝6平行，而y＝y（x）满足方程y″－2y′＋5y＝0，则此曲线的方程为（ ）。A
y＝excos2xB
y＝－excos2xC
y＝exsin2xD
y＝－exsin2x
热门标签
最新试卷