网友您好， 请在下方输入框内输入要搜索的题目：

题目内容 （请给出正确答案）
已知则f(x)ax：( )。

A、sinx+C
B、cosx+C
C、-cosx+sinx+C
D、cosx+sinx+C

参考答案

参考解析
解析：
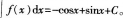
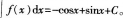
更多 “已知则f(x)ax：( )。A、sinx+C B、cosx+C C、-cosx+sinx+C D、cosx+sinx+C ” 相关考题
考题 ∫f(x)dx=F(x)＋C,a≠0,则∫f(b－ax)dx等于() A.F(b-ax)+CB.-(1/a)F(b-ax)+CC.aF(b-ax)+CD.(1/a)F(b-ax)+C
查看答案
考题 已知函数f（x）=x3 +ax2+b，曲线y=f（x）在点（1，1）处的切线为y=x．（I）求a，b；（II）求f（x）的单调区间，并说明它在各区间的单调性．
查看答案
考题 已知f(x)=x2+ax+3，若f(2+x)=f(2-x)，则f(2)=（）。A.0B.-1C.-2D.-3
查看答案
考题 数学运算已知f(x)＝x2+ax+3，若f(2+x)＝f(2-x)，则f(2)＝( )。A．0B．-1C．-2D．3
查看答案
考题 已知函数f(x)=(a+1)lnx+ax2+1.(Ⅰ)讨论函数f(x)的单调性；(Ⅱ)设a≤-2，证明：对任意x2,x2 (0,+∞)，|f(x1)-f(x2)|≥4|x1-x2|.
查看答案
考题 设f（x）、f'（x）为已知的连续函数，则微分方程y'+ f'（x）y = f（x）f'（x）的通解是：
查看答案
考题 已知函数f(x)在x=1处可导，则f'(1)等于： A. 2 B. 1
查看答案
考题 设y=f(x)是(a, b)内的可导函数，X,X+ΔX是(a, b)内的任意两点，则： (A) Δy= f‘ (x)Ax (B)在x，x+Ax之间恰好有一点ξ，使Δy=f'(ξ)Ax (C)在x, x+Ax之间至少有一点ξ，使Δy=f'(ξ)Ax (D)对于x，x+ax之间任意一点ξ，使Δy=f'(ξ)Ax
查看答案
考题 已知y=ax3在点x=1处的切线平行于直线y=2x-1，则a=______．
查看答案
考题 已知函数，则 A.Ax=0是f(x)的第一类间断点 B.x=0是f(x)的第二类间断点 C.f(x)在x=0处连续但不可导 D.f(x)在x=0处可导
查看答案
考题 设函数f（x）=2ax2-ax，且f（2）=-6，则a=（　　）A.-1 B.0 C.1 D.4
查看答案
考题 已知函数(x)=x5十ax3+bx-8且(-2)=10，则(2)等于（ ）A.-26 B.-18 C.-10 D.10
查看答案
考题 已知函数f(x)=cos，则下列等式中对于任意x都成立的是（）A.f(x+2π)=f(x) B.f(π-x)=f(x) C.f(-x)=f(x) D.f(-x)=-f(x)
查看答案
考题 已知函数f(x）=f(x+4),f(0）=0，且在（—2，2）上有f'(x)=|x|,则f(19)=
查看答案
考题 已知函数f(x)=∣2x-3∣+6，已知函数g(x)=kx+7，若f(x)与g(x)有且仅有一个交点，则k的值不可能为( )。
查看答案
考题 若函数f(x)=(k-1)ax- ax (a＞0且α≠1)在R上既是奇函数，又是减函数，则g(x)=loga (x+k)的图象是( )。
查看答案
考题 已知AX=836BH，X=FFFFH，执行“CMP AX, X”后，标志位ZF、CF、OF、SF=？
查看答案
考题 已知f（x）=2x3+5，则f[1，2，3，4]=（），f[1，2，3，4，5]=（）。
查看答案
考题 设a0，则当满足条件（）时，函数f（x）=ax3+3ax2+8为增函数。A、x-2B、-2C、x0D、x-2或x0
查看答案
考题 单选题已知f（x）＝x3＋ax2＋bx在x＝1处取得极小值－2，则a＝（　　），b＝（　　）。A 0；－3B 1；－3C 0；3D 1；3
查看答案
考题 填空题已知f（x）＝x3＋ax2＋bx在x＝－1处取得极小值－2，则a＝____，b＝____。
查看答案
考题 单选题设sinx/x为f（x）的一个原函数，且a≠0则∫[f（ax）/a]dx等于（　　）。A sinax/（a3x）＋CB sinax/（a2x）＋CC sinax/（ax）＋CD sinax/x＋C
查看答案
考题 填空题已知f′（ex）＝xe－x，且f（1）＝0，则f（x）＝____。
查看答案
考题 填空题设f（x，y）＝ax＋by，其中a，b为常数，则f[xy，f（x，y）]＝____。
查看答案
考题 单选题已知f（x）＝x3＋ax2＋bx在x＝－1处取得极小值－2，则a＝（　　），b＝（　　）。A a＝2；b＝3B a＝4；b＝5C a＝4；b＝3D a＝2；b＝5
查看答案
考题 单选题设a0，则当满足条件（）时，函数f（x）=ax3+3ax2+8为增函数。A x-2B -2C x0D x-2或x0
查看答案
考题 单选题设f（x，y）＝ax＋by，其中a，b为常数，则f[xy，f（x，y）]＝（　　）。A xy＋bx＋b2yB bxy＋ax＋byC bxy＋ax－byD axy＋abx＋b2y
查看答案
热门标签
最新试卷