网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设a,b是两个非零向量,则下面说法正确的是( )。
A.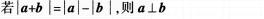
B.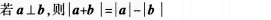
C.
D.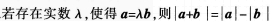
A.
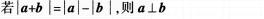
B.
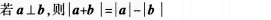
C.

D.
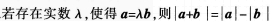
参考答案
参考解析
解析: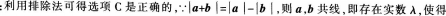

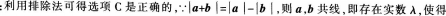

更多 “设a,b是两个非零向量,则下面说法正确的是( )。 A. B. C. D.” 相关考题
考题
设A,B为满足AB=0的任意两个非零矩阵,则必有(56)。A.A的列向量组线性相关,B的行向量组线性相关B.A的列向量组线性相关,B的列向量组线性相关C.A的行向量组线性相关,B的行向量组线性相关D.A的列向量组线性相关,B的列向量组线性相关
考题
设A为m×n矩阵,则齐次线性方程组Ax=0有非零解的充分必要条件是( )。
A、矩阵A的任意两个列向量线性相关
B、矩阵A的任意两个列向量线性无关
C、矩阵A的任一列向量是其余列向量的线性组合
D、矩阵A必有一个列向量是其余列向量的线性组合
考题
设A是mxn的非零矩阵,B是nxl非零矩阵,满足AB=0,以下选项中不一定成立的是:
A. A的行向量组线性相关 B. A的列向量组线性相关
C.B的行向量组线性相关 D.r(A)+r(B)≤n
考题
单选题设A为m×n矩阵,则齐次线性方程组Ax=0有非零解的充分必要条件是( )。[2017年真题]A
矩阵A的任意两个列向量线性相关B
矩阵A的任意两个列向量线性无关C
矩阵A的任一列向量是其余列向量的线性组合D
矩阵A必有一个列向量是其余列向量的线性组合
考题
单选题设a,b是两个非零向量,则下面说法正确的是( )。A
若|a+b|=|a|-|b|,则a⊥bB
若a⊥b,则|a+b|=|a|-|b|C
若|a+b|=|a|-|b|,则存在实数λ,使得a=λbD
若存在实数λ,使得a=λb,则|a+b|=|a|-|b|
考题
单选题设a(→),b(→)为非零向量,且a(→)⊥b(→),则必有( )。A
|a(→)+b(→)|=|a(→)|+|b(→)|B
|a(→)+b(→)|=|a(→)|-|b(→)|C
|a(→)+b(→)|=|a(→)-b(→)|D
a(→)+b(→)=a(→)-b(→)
考题
单选题设α、β均为非零向量,则下面结论正确的是( )。[2017年真题]A
α×β=0是α与β垂直的充要条件B
α·β=0是α与β平行的充要条件C
α×β=0是α与β平行的充要条件D
若α=λβ(λ是常数),则α·β=0
考题
单选题设A,B为满足AB=0(→)的任意两个非零矩阵,则必有( )。A
A的列向量组线性相关,B的行向量组线性相关B
A的列向量组线性相关,B的列向量组线性相关C
A的行向量组线性相关,B的行向量组线性相关D
A的行向量组线性相关,B的列向量组线性相关
考题
单选题设α,β,γ都是非零向量,α×β=α×γ,则()。A
β=γB
α∥β且α∥γC
α∥(β-γ)D
α⊥(β-γ)
热门标签
最新试卷