考题
设η为非零向量,A=,η为方程组AX=O的解,则a=_______,方程组的通解为_______.
考题
已知是线性方程组的解, 是它的导出组的解,求方程组的通解。
考题
设A=,且AX=0的基础解系含有两个线性无关的解向量,求AX=0的通解.
考题
设齐次线性方程组其中ab≠0,n≥2.讨论a,b取何值时,方程组只有零解、有无穷多个解?在有无穷多个解时求出其通解.
考题
当a,b取何值时,方程组无解、有唯一解、有无数个解?在有无数个解时求出其通解.
考题
设3阶实对称矩阵A的各行元素之和都为3,向量都是齐次线性方程组AX=0的解.① 求A的特征值和特征向量.② 求作正交矩阵Q和对角矩阵
考题
取何值时,非齐次线性方程组 (1)有唯一解 (2)无解 (3)有无穷多个解? 并在无穷多个解时,求方程组的通解。
考题
设有下列线性方程组(Ⅰ)和(Ⅱ) (Ⅰ) (Ⅱ) (1) 求方程组(Ⅰ)的通解; (2) 当方程组(Ⅱ)中的参数m,n,t为何值时,(Ⅰ)与(Ⅱ)同解?
考题
常数k取何值时, 方程组无解, 有惟一解或有无穷多解? 当方程组有无穷多解时求其通解
考题
已知非齐次线性方程组 有3个线性无关的解. (Ⅰ)证明方程组系数矩阵A的秩; (Ⅱ)求的值及方程组的通解
考题
设有齐次线性方程组
试问a为何值时,该方程组有非零解,并求其通解.
考题
问取何值时 非齐次线性方程组, (1)有唯一解 (2)无解 (3)有无穷多个解,并在无穷多个解时,求方程组的通解
考题
设(Ⅰ)和(Ⅱ)是两个四元齐次线性方程组,(Ⅰ)为,(Ⅱ)有一个基础解系(0,1,1,0)T,(-1,2,2,1)T.求(Ⅰ)和(Ⅱ)的全部公共解
考题
已知下列非齐次线性方程组(Ⅰ),(Ⅱ)
(1)求解方程组(Ⅰ),用其导出组的基础解系表示通解.
(2)当方程组中的参数m,n,t为何值时,方程组(Ⅰ)与(Ⅱ)同解.
考题
设矩阵且方程组无解, (Ⅰ)求a的值; (Ⅱ) 求方程组的通解
考题
设有齐次线性方程组.试问取何值时,该方程组有非零解,并求出其通解
考题
设(Ⅰ)和(Ⅱ)都是3元非齐次方程组,(Ⅰ)有通解;(Ⅱ)有通解。求(Ⅰ)和(Ⅱ) 的公共解
考题
讨论a、b为何值时非齐次线性方程组有无穷多解,并求其通解。
考题
设线性方程组与方程有公共解,求a的值及所有公共解
考题
设线性方程组(I)与(II)有公共的非零解,其中(I)为,(II)有基础解系,求p,t的值和全部公共解
考题
设3阶矩阵A=[α1,α2,α3]有3个不同的特征值,且a3=a1+2a2.
(Ⅰ)证明r(A)=2;
(Ⅱ)若β=α1,α2,α3,求方程组Ax=β的通解.
考题
设,.
已知线性方程组Ax=b存在2个不同的解.
(Ⅰ)求λ,a;
(Ⅱ)求方程组Ax=b的通解.
考题
设n元线性方程组Ax=b,其中
.
(Ⅰ)证明行列式|A|=(n+1)a^n;
(Ⅱ)当a为何值时,该方程组有唯一解,并求x1;
(Ⅲ)当a为何值时,该方程组有无穷多解,并求通解.
考题
已知齐次线性方程组(1)方程组仅有零解;(2)方程组有非零解,在有非零解时,求此方程组的一个基础解系.
考题
设(1)求lAl;
(2)已知线性方程组AX-b有无穷多解,求a,并求AX=b的通解。
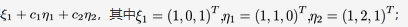 ;(Ⅱ)有通解
;(Ⅱ)有通解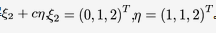 。求(Ⅰ)和(Ⅱ) 的公共解
。求(Ⅰ)和(Ⅱ) 的公共解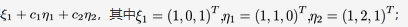 ;(Ⅱ)有通解
;(Ⅱ)有通解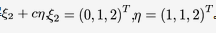 。求(Ⅰ)和(Ⅱ) 的公共解
。求(Ⅰ)和(Ⅱ) 的公共解
