网友您好， 请在下方输入框内输入要搜索的题目：

题目内容 （请给出正确答案）
若n阶矩阵A的任意一行中n个元素的和都是a，则A的一特征值为：

A. a
B. -a
C. 0
D. a-1

参考答案

参考解析
解析：解：本题主要考察两个知识点：特征值的求法及行列的运算。

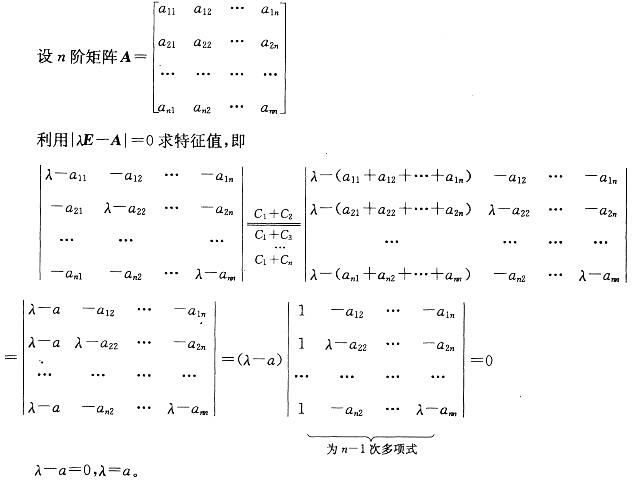
A的一特征值为a。
选A。
更多 “若n阶矩阵A的任意一行中n个元素的和都是a，则A的一特征值为： A. a B. -a C. 0 D. a-1 ” 相关考题
考题 可对角化的矩阵是____。 A.实对称阵B.有n个相异特征值的n阶阵C.有n个线性无关的特征向量的n阶方阵
查看答案
考题 下列命题为真的是A． 任意n阶无向图的最大度△≤nB．欧拉回路都是初级回路C．若无向图G是n阶m条边r个面的平面图，则n-m+r=2D．若T为非平凡的无向树，则T中每条边都是桥
查看答案
考题 若n阶矩阵A,B有共同的特征值,且各有n个线性无关的特征向量,则() A、A与B相似B、A≠B，但|A-B|=0C、A=BD、A与B不一定相似，但|A|=|B|
查看答案
考题 n阶单位矩阵的特征值都是1。() 此题为判断题(对，错)。
查看答案
考题 下列命题中为真的是A．任意n阶无向图的最大度≤nB．欧拉回路都是初级回路C．若无向图G是n阶m条边r个面的平面图，则n-m+1=2D．若T为非平凡的无向树，则T中每条边都是桥
查看答案
考题 设n阶矩阵A有一个特征值3，则|-3E+A|=_________.
查看答案
考题 设A为n阶对称矩阵,则A是正定矩阵的充分必要条件是( ). A.二次型xTAx的负惯性指数零B.存在n阶矩阵C,使得A=CTCC.A没有负特征值D.A与单位矩阵合同
查看答案
考题 设A为n阶实对称矩阵,则(). A.A的n个特征向量两两正交B.A的n个特征向量组成单位正交向量组C.A的k重特征值λ0,有r(λ0E-A)=n-kD.A的k重特征值λ。，有r(λ0E-A)=k
查看答案
考题 设A是n阶实对称矩阵，则A有n个()特征值.
查看答案
考题 若将N阶对称矩阵A按照行序为主序方式将包括主对角线元素在内的下三角形的所有元素依次存放在一个一维数组B中，则该对称矩阵在B中占用了(40)—个数组元素。(40)A．N2B．N×(N-1)C．N×(N+1)/2D．N×(N-1)/2
查看答案
考题 若n阶矩阵A的任意一行中n个元素的和都是a，则A的一特征值为： A. a B. -a C. 0 D. a-1
查看答案
考题 设A、B都是n阶可逆矩阵，则
查看答案
考题 与n阶单位矩阵E相似的矩阵是 A. B.对角矩阵D（主对角元素不为1） C.单位矩阵E D.任意n阶矩阵A
查看答案
考题 设n阶矩阵A与对角矩阵相似,则().A.A的n个特征值都是单值 B.A是可逆矩阵 C.A存在n个线性无关的特征向量 D.A一定为n阶实对称矩阵
查看答案
考题 n阶实对称矩阵A为正定矩阵，则下列不成立的是( )。A.所有k级子式为正(k=1，2，…，n) B.A的所有特征值非负 C. D.秩(A)=n
查看答案
考题 设A是n阶矩阵，且Ak=O(k为正整数)，则( )。A.A一定是零矩阵 B.A有不为0的特征值 C.A的特征值全为0 D.A有n个线性无关的特征向量
查看答案
考题 已知n阶可逆矩阵A的特征值为λ0，则矩阵(2A)-1的特征值是：
查看答案
考题 若n阶矩阵A，B有共同的特征值，且各有n个线性无关的特征向量，则（ ） A.A与B相似 B. C.A=B D.A与B不一定相似，但|A|=|B|
查看答案
考题 若n阶矩阵A的任意一行中n个元素的和都是a，则A的一特征值为： A. a B.-a C. 0 D. a-1
查看答案
考题 设A,B为n阶矩阵. 　　(1)是否有AB～BA；(2)若A有特征值1,2,…,n,证明：AB～BA.
查看答案
考题 设A为n阶矩阵,A的各行元素之和为0且r(A)=n-1,则方程组AX=0的通解为_______.
查看答案
考题 设A为m×n阶实矩阵,且r(A)=n.证明：A^TA的特征值全大于零.
查看答案
考题 设n阶方阵是一个上三角矩阵，则需存储的元素个数为()。A.n B.n×n C.n×n/2 D.n(n+1)/2
查看答案
考题 若一个n阶矩阵A中的元素满足：Aij=Aji（0=I，j=n-1）则称A为（）矩阵；若主对角线上方（或下方）的所有元素均为零时，称该矩阵为（）。
查看答案
考题 n阶实对称矩阵A为正定矩阵，则下列不成立的是（）。A、所有k级子式为正（k=1，2，…，n）B、A的所有特征值非负C、秩（A）=n
查看答案
考题 单选题设A为n阶方阵，若对任意n×m（m≥n）矩阵B都有AB＝0，则A＝（　　）。A 0B 1C 2D 3
查看答案
考题 填空题设A为n阶方阵，若对任意n×m（m≥n）矩阵B都有AB=0，则A=____.
查看答案
考题 填空题若一个n阶矩阵A中的元素满足：Aij=Aji（0=I，j=n-1）则称A为（）矩阵；若主对角线上方（或下方）的所有元素均为零时，称该矩阵为（）。
查看答案
热门标签
最新试卷