网友您好， 请在下方输入框内输入要搜索的题目：
题目内容
（请给出正确答案）
矩阵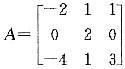
对应特征值λ=-1的全部特征向量为( )。
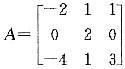对应特征值λ=-1的全部特征向量为( )。参考答案
参考解析
解析：λ=-1时，解方程组(A+E)X=0，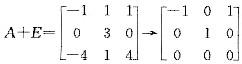
，得基础解系
，故全部特征向量为
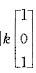(k≠0)
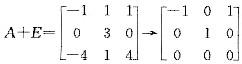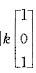，得基础解系，故全部特征向量为(k≠0)
更多 “矩阵对应特征值λ=-1的全部特征向量为( )。” 相关考题
考题
n*n矩阵可看作是n维空间中的线性变换，矩阵的特征向量经过线性变换后，只是乘以某个常数(特征值)，因此，特征向量和特征值在应用中具有重要的作用。下面的矩阵(其中w1、w2、w3均为正整数)有特征向量(w1，w2，w3)，其对应的特征值为( )。A．1／3B．1C．3D．9
考题
设三阶矩阵A的特征值为λ1=1,λ2=0,λ3=1,则下列结论不正确的是().A.矩阵A不可逆
B.矩阵A的迹为零
C.特征值-1,1对应的特征向量正交
D.方程组AX=0的基础解系含有一个线性无关的解向量
考题
设A是3阶实对称矩阵，P是3阶可逆矩阵，B=P-1AP，已知a是A的属于特征值λ的特征向量，则B的属于特征值λ的特征向量是：
A. Pa B. P-1A C. PTa D.（P-1）Ta
考题
设A是3阶实对称矩阵，P是3阶可逆矩阵，B=P-1AP，已知α是A的属于特征值λ的特征向量，则B的属于特征值λ的特征向量是：(A) Pα (B) P-1α (C) PTa (D) P(-1)Ta
考题
设λ1，λ2是矩阵A的两个不同的特征值，对应的特征向量分别为α1，α2，则α1，A(α1+α2)线性无关的充分必要条件是( )。
A、λ1=0
B、λ2=0
C、λ1≠0
D、λ2≠0
考题
设n阶矩阵A可逆，α是A的属于特征值λ的特征向量，则下列结论中不正确的是（）。A、α是矩阵-2A的属于特征值-2λ的特征向量B、α是矩阵的属于特征值的特征向量C、α是矩阵A*的属于特征值的特征向量D、α是矩阵AT的属于特征值λ的特征向量
考题
已知3维列向量α，β满足αTβ=3，设3阶矩阵A=βαT，则（）。A、β是A的属于特征值0的特征向量B、α是A的属于特征值0的特征向量C、β是A的属于特征值3的特征向量D、α是A的属于特征值3的特征向量
考题
单选题设A是三阶矩阵，α1=（1，0，1）T，α2=（1，1，0）T是A的属于特征值1的特征向量，α3=（0，1，2）T是A的属于特征值-1的特征向量，则：（）A
α1-α2是A的属于特征值1的特征向量B
α1-α3是A的属于特征值1的特征向量C
α1-α3是A的属于特征值2的特征向量D
α1+α2+α3是A的属于特征值1的特征向量
考题
单选题设n阶矩阵A可逆，α是A的属于特征值λ的特征向量，则下列结论中不正确的是（）。A
α是矩阵-2A的属于特征值-2λ的特征向量B
α是矩阵的属于特征值的特征向量C
α是矩阵A*的属于特征值的特征向量D
α是矩阵AT的属于特征值λ的特征向量
考题
问答题证明： （1）若α(→)1，α(→)2，…，α(→)r是A的属于特征值λ的特征向量，则α(→)1，α(→)2，…，α(→)r的任一个非零线性组合也是A的属于λ的特征向量。 （2）矩阵可逆的充分必要条件是它的特征值都不为0。
考题
单选题已知3维列向量α，β满足αTβ=3，设3阶矩阵A=βαT，则（）。A
β是A的属于特征值0的特征向量B
α是A的属于特征值0的特征向量C
β是A的属于特征值3的特征向量D
α是A的属于特征值3的特征向量
考题
单选题（2009）设A是3阶实对称矩阵，P是3阶可逆矩阵，B=P-1AP，已知α是A的属于特征值λ的特征向量，则B的属于特征值λ的特征向量是：（）A
PαB
P-1αC
PTαD
（P-1）Tα
考题
问答题设有三个非零的n阶（n≥3）方阵A1、A2、A3，满足Ai2＝Ai（i＝1，2，3），且AiAj＝0（i≠j，i、j＝1，2，3），证明： （1）Ai（i＝1，2，3）的特征值有且仅有0和1； （2）Ai的对应于特征值1的特征向量是Aj的对应于特征值0的特征向量（i≠j）； （3）若α(→)1、α(→)2、α(→)3分别为A1、A2、A3的对应于特征值1的特征向量，则向量组α(→)1、α(→)2、α(→)3线性无关。
热门标签
最新试卷
