网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设随机变量X,Y不相关,X~U(-3,3),Y的密度为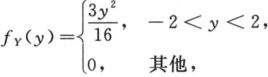 根据切比雪夫不等式,有P{|X-Y|<3)≥_______.
根据切比雪夫不等式,有P{|X-Y|<3)≥_______.
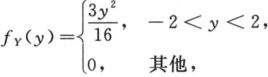 根据切比雪夫不等式,有P{|X-Y|<3)≥_______.
根据切比雪夫不等式,有P{|X-Y|<3)≥_______.参考答案
参考解析
解析:E(x)=0,D(x)=3,E(Y)=0,D(Y)=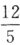 ,则E(X-Y)=0,D(X-Y)=D(X)+D(Y)-2Cov(X,Y)=
,则E(X-Y)=0,D(X-Y)=D(X)+D(Y)-2Cov(X,Y)=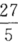 ,所以P(|X-Y|<3)=P(|(X-Y)-E(x-Y)|<3)≥1
,所以P(|X-Y|<3)=P(|(X-Y)-E(x-Y)|<3)≥1
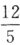 ,则E(X-Y)=0,D(X-Y)=D(X)+D(Y)-2Cov(X,Y)=
,则E(X-Y)=0,D(X-Y)=D(X)+D(Y)-2Cov(X,Y)=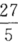 ,所以P(|X-Y|<3)=P(|(X-Y)-E(x-Y)|<3)≥1
,所以P(|X-Y|<3)=P(|(X-Y)-E(x-Y)|<3)≥1
更多 “设随机变量X,Y不相关,X~U(-3,3),Y的密度为根据切比雪夫不等式,有P{|X-Y|” 相关考题
考题
(1)将一均匀的骰子连续扔六次,所出现的点数之和为X,用切比雪夫不等式估计P(14 (2)设随机变量X1,X2,…,X10相互独立且Xi~π(i)(i=1,2,…,10),,根据切比雪夫不等式,P{4
考题
设随机变量X与Y相互独立,X服从参数为1的指数分布,Y的概率分布为P{Y=-1}=p,P{Y=1)=1-p,(0 (Ⅰ)求Z的概率密度;
(Ⅱ)p为何值时,X与Z不相关;
(Ⅲ)X与Z是否相互独立?
考题
设随机变量X和Y的数学期望分别为-2和2,方差分别为1和4,而相关系数为-0.5,则根据切比雪夫不等式P{|X+Y|≥6}≤()。
热门标签
最新试卷