网友您好， 请在下方输入框内输入要搜索的题目：

题目内容 （请给出正确答案）
求二元函数(x，y)=x2+y2+xy在条件x+2y=4下的极值．

参考答案

参考解析
解析：解设F((x，y，λ)=(x，y)+λ(x+2y-4)=x2+y2+xy+λ(x+2y-4)，
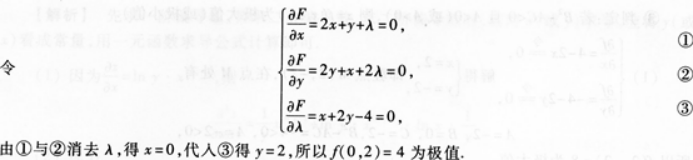
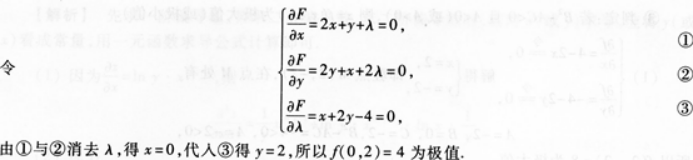
更多 “求二元函数(x，y)=x2+y2+xy在条件x+2y=4下的极值．” 相关考题
考题 求函数y=x-ln(1+x)的极值.
查看答案
考题 以下结论正确的是()。 A、若x0为函数y=f(x)的驻点,则x0必为函数y=f(x)的极值点.B、函数y=f(x)导数不存在的点,一定不是函数y=f(x)的极值点.C、若函数y=f(x)在x0处取得极值,且f′(x)存在,则必有f′(x)=0.D、若函数y=f(x)在x0处连续,则y=f′(x0)一定存在.
查看答案
考题 (本题满分8分)求函数y＝x3-3x2-1的单调区间、极值及其曲线的凹凸区间和拐点。
查看答案
考题 求函数y=x3-3x2-9x＋1的极值．
查看答案
考题 二元函数f(x,y)在点(x ,y)偏导数存在是f(x,y)在该点连续的() A、充分必要条件B、必要而非充分条件C、充分而非必要条件D、既非充分又非必要条件
查看答案
考题 求函数z=x2+2y2+4x-8y+2的极值．
查看答案
考题 求函数(x，y)=x2+y2在条件2x+3y=1下的极值．
查看答案
考题 设函数f(x，y)=X2+Y2+xy+3，求f(x，y)的极值点与极值．
查看答案
考题 求y=f(x)=2x3-3x2-12x+14的极值点和极值，以及函数曲线的凸凹性区间和拐点.
查看答案
考题 求函数z=x2+y2+2y的极值．
查看答案
考题 求函数z=x2-xy+y2+9x一6y+20的极值．
查看答案
考题 求函数(x，y)=x3+y3在条件x2+2y2=1下的最值．
查看答案
考题 已知函数(x)=x4-4x+1． (1)求(x)的单调区间和极值； (2)求曲线y=(x)的凹凸区间．
查看答案
考题 求函数(x，y)=4(x-y)-x2-y2的极值．
查看答案
考题 设随机变量X,y相互独立,且X～,Y～E(4),令U=X+2Y,求U的概率密度.
查看答案
考题 设二维随机变量(X,Y)的联合密度函数为f(x,y)= 　　(1)求随机变量X,Y的边缘密度函数； 　　(2)判断随机变量X,Y是否相互独立； 　　(3)求随机变量Z=X+2Y的分布函数和密度函数.
查看答案
考题 设z=z(x,y)是由 确定的函数，求 的极值点和极值
查看答案
考题 设随机变量X～U(0,1),在X=x(0　　(1)求X,y的联合密度函数； 　　(2)求y的边缘密度函数.
查看答案
考题 求二元函数的极值。
查看答案
考题 已知函数y(x)由方程x^3+y^3-3x+3y-2=0确定，求y(x)的极值.
查看答案
考题 设函数y=f(x)由方程y^3+xy^2+x^2y+6=0确定，求f(x)的极值.
查看答案
考题 设函数y(x)是微分方程满足条件y(0)=0的特解. 　　(Ⅰ)求y(x)； 　　(Ⅱ)求曲线y=y(x)的凹凸区间及拐点.
查看答案
考题 求二元函数f(x，y)=x^2(2+y^2)+ylny的极值.
查看答案
考题 求函数f(x，y)=e2x(x+y2+2y)的极值.?
查看答案
考题 下列各点中为二元函数z=x3-y3-3x2+3y-9x的极值点的是（）。A、（3，-1）B、（3，1）C、（1，1）D、（-1，-1）
查看答案
考题 问答题求由方程x2＋y2＋z2－xz－yz－2x－2y＋2z－6＝0确定的函数z＝z（x，y）的极值。
查看答案
考题 单选题（2010）下列各点中为二元函数z=x3-y3-3x2+3y-9x的极值点的是：（）A （3，-1）B （3，1）C （1，1）D （-1，-1）
查看答案
热门标签
最新试卷