网友您好， 请在下方输入框内输入要搜索的题目：

题目内容 （请给出正确答案）
在抛物线y=1-x2与x轴所围成的平面区域内作一内接矩形ABCD，其一边AB在x轴上(如图1-2-4所示)．设AB=2x，矩形面积为S(x)．

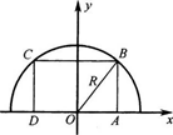
图1—2—3

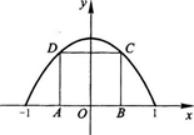
图1—2—4
①写出S(x)的表达式；
②求S(x)的最大值．

参考答案

参考解析
解析：①S(x)=AB·BC=2xy=2x(1-x2)(0
更多 “在抛物线y=1-x2与x轴所围成的平面区域内作一内接矩形ABCD，其一边AB在x轴上(如图1-2-4所示)．设AB=2x，矩形面积为S(x)． 图1—2—3 图1—2—4 ①写出S(x)的表达式； ②求S(x)的最大值．” 相关考题
考题 设（X，Y）服从在区域D上的均匀分布，其中D为x轴、y轴及x+y=1所围成，求X与Y的协方差Cov(X,Y).
查看答案
考题 曲线y=sinx在[-π，π]上与x轴所围成的图形的面积为( )。A.2 B.0 C.4 D.6
查看答案
考题 如图15所示矩形截面中阴影部分面积对x轴的面积矩Sx的值为( )。
查看答案
考题 已知D为x轴、y轴和抛物线y＝1－x2所围成的在第一象限内的闭区域，则
查看答案
考题 D 域由 x 轴，x2 + y2 ? 2x = 0( y ≥ 0)及 x+y=2 所围成， f (x, y)是连续函数，化
查看答案
考题 设抛物线y=1-x2与x轴的交点为A，B，在它们所围成的平面区域内，以线段AB为下底作内接等腰梯形ABCD(如图1—2-2所示)．设梯形上底CD长为2x，面积为S(x)． 图1一2—1 图1—2—2 ①写出S(x)的表达式； ②求S(x)的最大值．
查看答案
考题 设曲线y=4-x2(x≥0)与x轴，y轴及直线x=4所围成的平面图形为D(如 图1—3—2中阴影部分所示)． 图1—3—1 图1—3—2 ①求D的面积S； ②求图中x轴上方的阴影部分绕y轴旋转一周所得旋转体的体积Vy．
查看答案
考题 已知函数(x)=-x2+2x． ①求曲线y=(x)与x轴所围成的平面图形面积S； ②求①的平面图形绕x轴旋转一周所得旋转体体积Vx．
查看答案
考题 ①求由曲线y=x，y=1/x，x=2与y=0所围成的平面图形的面积S； ②求①中的平面图形绕x轴旋转一周所得旋转体的体积V．
查看答案
考题 ①求曲线y=x2(x≥0)，y=1与x=0所围成的平面图形的面积S： ②求①中的平面图形绕Y轴旋转一周所得旋转体的体积Vy．
查看答案
考题 设D为曲线y=1-x2，直线y=x+1及x轴所围成的平面区域(如图1-3—1所示)· ①求平面图形的面积； ②求平面图形D绕x轴旋转一周所成旋转体的体积Vx．
查看答案
考题 由曲线y=x3，直线x=1，z轴围成的平面有界区域的面积为_________．
查看答案
考题 ①求曲线y=ex及直线x=1，x=0，y=0所围成的图形D的面积S： ②求平面图形D绕x轴旋转一周所成旋转体的体积Vx．
查看答案
考题 曲线y=1-x2与x轴所围成的平面图形的面积S=()·A.2 B.4/3 C.1 D.2/3
查看答案
考题 求曲线y=x2与直线y=0，x=1所围成的平面图形绕x轴旋转一周所得旋转体的体积．
查看答案
考题 ①求在区间(0，π)上的曲线y=sinx与x轴所围成图形的面积S； ②求①中的平面图形绕x轴旋转一周所得旋转体的体积Vx．
查看答案
考题 如图，已知圆C与x轴相切于点T(1，0)，与y轴正半轴交于两点A，B(B在A的上方)且AB=2，则圆C在点8处的切线在x轴上的截距_________。
查看答案
考题 设f(x，y)为连续函数，且满足，其中D是由x轴、y轴、所围成的闭区域
查看答案
考题 将平面曲线y=x2分别绕y轴和x轴旋转一周，所得旋转曲面分别记作S1和S2。 (1)在空间直角坐标系中，分别写出曲面S1和S2的方程； (2)求平面y=4与曲面S1。所围成的立体的体积。
查看答案
考题 曲线y=sinx在[-π,π]上与x轴所围成的图形的面积为（ ）。 A. 2 B. 0 C. 4 D. 6
查看答案
考题 设抛物线Y=1-x2与x轴的交点为A、B，在抛物线与x轴所围成的平面区域内，以线段AB为下底作内接等腰梯形ABCD(如图2—1所示)．设梯形上底CD长为2x，面积为 S(x)． (1)写出S(x)的表达式； (2)求S(x)的最大值．
查看答案
考题 ，其中区域如图5-3所示，由y=x，y=1与Y轴围成．
查看答案
考题 设D为曲线y=x2与直线y=x所围成的有界平面图形，求D绕x轴旋转一周所得旋转体的体积V.?
查看答案
考题 (1)求曲线Y=ex及直线x=1，x=0,y=0所围成的平面图形(如图3—3所示) 的面积A． (2)求(1)中平面图形绕x轴旋转一周所得旋转体的体积Vx.
查看答案
考题 由函数y=ex的图象与y=-2x，x=1，x=3所围成的封闭面积为_______。
查看答案
考题 曲线y=sinx在［-π，π]上与x轴所围成的图形的面积为（）。A、2B、0C、4D、6
查看答案
考题 问答题计算抛物线y2=2x与直线y=x-4所围成平面图形
查看答案
热门标签
最新试卷