网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设随机变量X的概率密度f(x)满足f(1+x)=f(1-x),且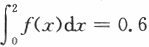 =
=
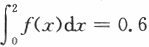 =
=
A.A0.2
B.0.3
C.0.4
D.0.5
B.0.3
C.0.4
D.0.5
参考答案
参考解析
解析:

更多 “设随机变量X的概率密度f(x)满足f(1+x)=f(1-x),且= A.A0.2 B.0.3 C.0.4 D.0.5 ” 相关考题
考题
设连续型随机变量X的密度函数为f(x),分布函数为F(x).如果随机变量X与-X分布函数相同,则().
A.F(z)=F(-x)
B.F(x)=F(-x)
C.F(X)=F(-x)
D.f(x)=f(-x)
考题
若∫f(x)dx=F(x)+C,则∫xf(1-x^2)dx=( )。
A. F(1-x^2)+C
B. -(1/2)F(1-x^2)+C
C. (1/2)F(1-x^2)+C
D. -(1/2)F(x)+C
考题
设随机变量X,Y独立同分布,且X的分布函数为F(x),则Z=max{X,Y}的分布函数为
A.AF^2(x)
B.F(x)F(y)
C.1-[1-F(x)]^2
D.[1-F(x)][1-F(y)]
考题
设F1(x)与F2(x)为两个分布函数,其相应的概率密度f1(x)与f2(x)是连续函数,则必为概率密度的是
A.Af1(x)f2(x)
B.2f2(x)F1(x)
C.f1(x)F2(x)
D.f1(x)F2(x)+f2(x)f1(x)
考题
设4/(1-x2)·f(x)=d/dx[f(x)]2,且f(0)=0,则f(x)等于:()A、(1+x)/(1-x)+cB、(1-x)/(1+x)+cC、1n|(1+x)/(1-x)|+cD、1n|(1-x)/(1+x)|+c
考题
设f(x)的二阶导数存在,且f′(x)=f(1-x),则下列式中何式可成立()?A、f″(x)+f′(x)=0B、f″(x)-f′(x)=0C、f″(x)+f(x)=0D、f″(x)-f(x)=0
考题
设随机变量X的概率密度和分布函数分别是f(x)和F(x),且f(x)=f(-x),则对任意实数a,有F(-a)=()A、1/2-F(a)B、1/2+F(a)C、2F(a)-1D、1-F(a)
考题
设F1(x)与F2(x)为两个分布函数,其相应的概率密度f1(x)与f2(x)是连续函数,则必为概率密度的是()A、f1(x)f2(x)B、2f2(x)F1(x)C、f1(x)F2(x)D、f1(x)F2(x)+f2(x)F1(x)
考题
设X1,X2是任意两个相互独立的连续型随机变量,它们的概率密度分别为f1(x)与f2(x),分布函数分别为F1(x)与F2(x),则()A、f1(x)+f2(x)必为某一随机变量的概率密度B、f1(x)f2(x)必为某一随机变量的概率密度C、F1(x)+F2(x)必为某一随机变量的分布函数D、F1(x)F2(x)必为某一随机变量的分布函数
考题
设随机变量X,Y独立同分布,且X的分布函数为F(x),则Z=max{X,Y}的分布函数为()A、F2(x)B、F(x)F(y)C、1-[1-F(x)]2D、[1-F(x)][1-F(y)]
考题
单选题设4/(1-x2)·f(x)=d/dx[f(x)]2,且f(0)=0,则f(x)等于:()A
(1+x)/(1-x)+cB
(1-x)/(1+x)+cC
1n|(1+x)/(1-x)|+cD
1n|(1-x)/(1+x)|+c
考题
单选题设f(x)的二阶导数存在,且f′(x)=f(1-x),则下列式中何式可成立()?A
f″(x)+f′(x)=0B
f″(x)-f′(x)=0C
f″(x)+f(x)=0D
f″(x)-f(x)=0
热门标签
最新试卷