网友您好， 请在下方输入框内输入要搜索的题目：

题目内容 （请给出正确答案）
I=∮C|y|ds的值为下列( )项，其中C：(x2+y2)2=a2(x2-y2)，a＞0。


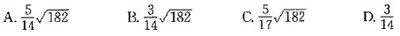
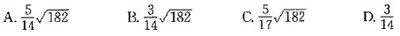
参考答案

参考解析
解析：曲线C可采用极坐标方程形式，然后根据曲线C及被积函数|y|关于x轴、y轴的对称性可得解
更多 “I=∮C|y|ds的值为下列( )项，其中C：(x2+y2)2=a2(x2-y2)，a＞0。 ” 相关考题
考题 设平面薄板所占xOy平面上的区域D为1≤x2+y2≤4，*≥0，y≥0，其面密度为π(x，y)=x2+y2，求该薄板的质量m。
查看答案
考题 设z=f（x2－y2），则dz 等于： A. 2x－2y B. 2xdx－2ydy C. f’（x2－y2）dx D.2f’（x2－y2）（xdx—ydy）
查看答案
考题 是由曲面z=x2+y2，y=x，y=0，z=1在第一
查看答案
考题 设z=f(x2-y2)，则dz 等于： A. 2x-2y B. 2xdx-2ydy C. f'(x2-y2)dx D. 2f'(x2-y2)(xdx-ydy)
查看答案
考题 (其中D:x2+y2≤1)化为极坐标系下的二次积分，其形式为下列哪一式？
查看答案
考题 圆x2＋y2＝25上的点到直线5x＋12y－169＝0的距离的最小值是（　　）A.9 B.8 C.7 D.6
查看答案
考题 设z=f(x2-y2)，则dz 等于： A. 2x-2y B. 2xdx-2ydy C. f'(x2-y2)dx D. 2f'(x2-y2)(xdx-ydy)
查看答案
考题 计算,其中Ω为z2=x2+y2，z=1所围成的立体，则正确的解法是( )。
查看答案
考题 将 (其中D：x2+y2≤1)化为极坐标系下的二次积分，其形式为( )。
查看答案
考题 设平面薄板所占Oxy平面上的区域D为1≤x2+y2≤4，x≥0，y≥0，其面密度 u(x，y)=2+y2，求该薄板的质量m．
查看答案
考题 已知X1=+0010100，Y1=+0100001，X2=0010100，Y2=0100001，试计算下列各式（设字长为8位）。 （1）[X1＋Y1]补=[X1]补＋[Y1]补=（） （2）[X1－Y2]补=[X1]补＋[－Y2]补=（） （3）[X2－Y2]补=[X2]补＋[－Y2]补=（） （4）[X2＋Y2]补=[X2]补＋[Y2]补=（）
查看答案
考题 设C为圆周x2+y2=ax（a0），则曲线积分的值是（）．A、a2B、2a2C、3a2D、4a2
查看答案
考题 设z=f（x2+y2），其中f具有二阶导数，则等于（）．A、2f’（x2+y2）B、4x2f"（x2+y2）C、2’（x2+y2）+4x2f"（x2+y2）D、2xf"（x2+y2）
查看答案
考题 填空题设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝____。
查看答案
考题 单选题与一族曲线中的每一条都交成直角的曲线叫做所给曲线族的正交轨线，若曲线族为x2＋y2＝2cx（c为常数），则此曲线族的正交轨线为（　　）。A y＝c1（x2＋y2）B y＝c1（x＋y）C y＝2c1（x2＋y2）D y＝c1（x2＋y2）/2
查看答案
考题 单选题设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝（　　）。A 1/5B 1/7C －1/7D －1/5
查看答案
考题 单选题设z=f（x2+y2），其中f具有二阶导数，则等于（）．A 2f’（x2+y2）B 4x2f（x2+y2）C 2’（x2+y2）+4x2f（x2+y2）D 2xf（x2+y2）
查看答案
考题 单选题∫L（x2＋y2＋2x）ds＝（　　），其中曲线L为x2＋y2＝R2A πR3B 2πR3C 4πR3D 6πR3
查看答案
考题 单选题∫L（x2＋y2＋2x）ds＝（　　），其中曲线L为x2＋y2＝R2A 2πR3/3B 2πR3C 4πR3D πR3
查看答案
考题 单选题已知流速场ux＝ax，uy＝－ay，uz＝0，求流函数ψ（　　）。A 无ψB ψ＝a（x2－y2）C ψ＝a（x2＋y2）D ψ＝axy
查看答案
考题 单选题设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝（　　）。A 1B －1C 1/7D －1/7
查看答案
考题 单选题设z＝φ（x2－y2），其中φ有连续导数，则函数z满足（　　）。A x∂z/∂x＋y∂z/∂y＝0B x∂z/∂x－y∂z/∂y＝0C y∂z/∂x＋x∂z/∂y＝0D y∂z/∂x－x∂z/∂y＝0
查看答案
考题 单选题设C为圆周x2+y2=ax（a0），则曲线积分的值是（）．A a2B 2a2C 3a2D 4a2
查看答案
考题 单选题I＝∮L（－ydx＋xdy）/（x2＋y2），因为∂Q/∂x＝∂P/∂y＝（y2－x2）/（x2＋y2）2，所以（　　）。A 对任意闭曲线L，I＝0B 在L为不含原点在内的闭区域的边界线时I＝0C 因为∂Q/∂x＝∂P/∂y在原点不存在，故对任意L，I≠0D 在L含原点在内时I＝0，不含原点时I≠0
查看答案
考题 填空题∫L（x2＋y2＋2x）ds＝____，其中曲线L为x2＋y2＝R2
查看答案
考题 问答题设z＝f（x2－y2，exy），其中f具有连续二阶偏导数，求∂z/∂x，∂z/∂y。
查看答案
考题 单选题设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝（　　）。A －1/2B －1/4C －1/7D －1/9
查看答案
热门标签
最新试卷