网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
设z=f(x2-y2),则dz 等于:
A. 2x-2y B. 2xdx-2ydy
C. f'(x2-y2)dx D. 2f'(x2-y2)(xdx-ydy)
A. 2x-2y B. 2xdx-2ydy
C. f'(x2-y2)dx D. 2f'(x2-y2)(xdx-ydy)
参考答案
参考解析
解析:提示:本题为二元函数求全微分的题目,计算公式为
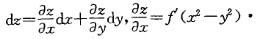
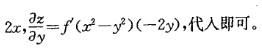
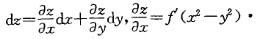
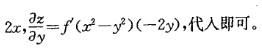
更多 “设z=f(x2-y2),则dz 等于: A. 2x-2y B. 2xdx-2ydy C. f'(x2-y2)dx D. 2f'(x2-y2)(xdx-ydy)” 相关考题
考题
单选题设函数f(u)可微,且f′(0)=1/2,则z=f(4x2-y2)在点(1,2)处的全微分dz|(1,2)=( )。A
4dx+2dyB
4dx-2dyC
-4dx+2dyD
-4dx-2dy
考题
单选题设方程x2+y2+z2=4z确定可微函数z=z(x,y),则全微分dz等于( )。[2014年真题]A
(ydx+xdy)/(2-z)B
(xdx+ydy)/(2-z)C
(dx+dy)/(2+z)D
(dx-dy)/(2-z)
考题
单选题设z=φ(x2-y2),其中φ有连续导数,则函数z满足( )。A
x∂z/∂x+y∂z/∂y=0B
x∂z/∂x-y∂z/∂y=0C
y∂z/∂x+x∂z/∂y=0D
y∂z/∂x-x∂z/∂y=0
考题
单选题设z=z(x,y)是由方程xz-xy+ln(xyz)=0所确定的可微函数,则∂z/∂y等于( )。[2013年真题]A
-xz/(xz+1)B
-x+1/2C
z(-xz+y)/[x(xz+1)]D
z(xy-1)/[y(xz+1)]
考题
单选题若z=f(x,y)和y=φ(x)均可微,则dz/dx等于( )。[2013年真题]A
∂f/∂x+∂f/∂yB
∂f/∂x+(∂f/∂y)(dφ/dx)C
(∂f/∂y)(dφ/dx)D
∂f/∂x-(∂f/∂y)(dφ/dx)
考题
单选题设函数z=f(x,y)的全微分为dz=xdx+ydy,则点(0,0)( )。A
不是f(x,y)的连续点B
不是f(x,y)的极值点C
是f(x,y)的极大值点D
是f(x,y)的极小值点
考题
单选题(2009)设z=f(x2-y2),则dz等于:()A
2x-2yB
2xdx-2ydyC
f′(x2-y2)dxD
2f′(x2-y2)(xdx-ydy)
热门标签
最新试卷