网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.
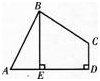
(1)求证:AB=BC;
(2)当BE⊥AD于E时,试证明:BE=AE+CD.

(1)求证:AB=BC;
(2)当BE⊥AD于E时,试证明:BE=AE+CD.
参考答案
参考解析
解析: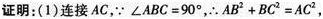
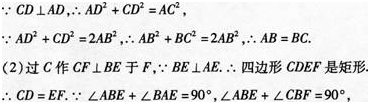

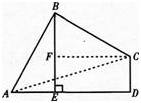
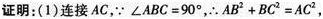
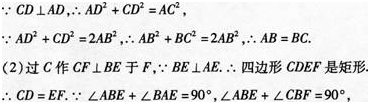


更多 “如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2. (1)求证:AB=BC; (2)当BE⊥AD于E时,试证明:BE=AE+CD. ” 相关考题
考题
在平行四边形ABCD中,∠DAB=60°,AB=15cm.已知⊙O的半径等于3cm,AB,AD分别与⊙O相切于点E,F,⊙O在平行四边形ABCD内沿AB方向滚动,与BC边相切时运动停止,试求⊙O滚过的路程.
考题
下面程序的输出是______。 char s[]="ABCD"; main() { char *p; for(p=s;p<s+4;p++) printf("%s\n",p); }A.ABCD BCD CD DB.A B C DC.D C B AD.ABCD ABC AB A
考题
对边相等,对角相等的凸四边形,是平行四边形吧?
方法①∠B小于90°;左上为A,左下为B,右下为C,右上为D;已知∠B=∠D;AB=CD;证明:过A作AN⊥BC于N;过C作CM⊥AD于M;连接AC∵AN⊥BC;CM⊥AD∴∠ANB=∠DMC=90°又∵∠B=∠D;AB=CD∴△ANB=△DMC(AAS)∴AN=CM;BN=DM又∵∠ANB=∠DMC=90°,AC=AC∴△ACD=△AMD(HL)∴AM=DN又∵BN=DM∴BD=AC∵BD=AC;AB=CD∴凸四边形ABCD为平行四边型。方法②∠B大于90°左上为A,左下为B,右下为C,右上为D;已知∠B=∠D;AB=CD;证明:延长CD,过A作AN⊥BC于N;延长AB,过C作CM⊥AD于M;连接AC∵AN⊥BC;CM⊥AD∴∠ANB=∠DMC=90°又∵∠B=∠D;AB=CD∴△ANB=△DMC(AAS)∴AN=CM;BN=DM又∵∠ANB=∠DMC=90°,AC=AC∴△ACD=△AMD(HL)∴AM=DN又∵BN=DM∴BD=AC∵BD=AC;AB=CD∴凸四边形ABCD为平行四边型。方法③∠B等于90°证明:∵∠B=∠D=90°;AB=CD;AC=AC∴△ABC=△ADC(HL)∴AB=CB∵BD=AC;AB=CD∴凸四边形ABCD为平行四边型。有错吗?若我的证明有错请明示,我知道有个反例,但它是凹四边形。
考题
下面程序的输出结果是( )。 char s()="ABCD",*p; main() { for(p=s;p<s+4;p++)printf("%s\n",p); )A.ABCD BCD CD DB.A B C DC.D C B AD.ABCD ABC AB A
考题
如图,D是△ABC内的一点,BD⊥CD,AD=6,BD=8,CD=6,E,F,G,H分别是AB,AC,CD, BD的中点.则四边形EFGH的周长是()。
A.12
B.14
C.15
D.16
考题
如图,平行四边形ABCD的面积是54平方厘米,点E、F、G分别是平行四边形ABCD边上的中点,H为AD边上的任意一点,则阴影部分的面积为( )平方厘米。
A. 27
B. 28
C. 32
D. 36
考题
如图,在一张矩形纸片ABCD中,AB=4,BC=8。点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点日处,点D落在G处,有以下四个结论:①四边形CFHE是菱形;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;④当点H与点A重合时, 。以上结论中,你认为正确的有( )个。
A.1
B.2
C.3
D.4
考题
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90o,E是CD的中点。
(1)证明:CD⊥平面PAE;
(2)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求四棱锥P-ABCD的体积。
考题
在VFP命令窗口输入?“ABC”$”ABCD”,结果是()A、”ABABCD”B、“CD”C、TD、F
热门标签
最新试卷