网友您好， 请在下方输入框内输入要搜索的题目：

题目内容 （请给出正确答案）
设A为可遵矩阵，k≠O，则下述结论不正确的是（ ）.《》（ ）


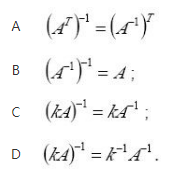
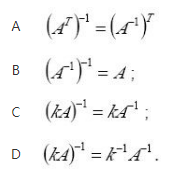
参考答案

参考解析
解析：
更多 “设A为可遵矩阵，k≠O，则下述结论不正确的是（ ）.《》（ ） ” 相关考题
考题 下列结论或等式正确的是()。 A.若A，B均为零矩阵，则有A=BB.矩阵乘法满足交换律，则(AB)k=AkBkC.对角矩阵是对称矩阵D.若A≠0，B≠0，则AB≠0
查看答案
考题 设λ0是矩阵A的特征方程的3重根,A的属于λ0的线性无关的特征向量的个数为k,则必有() A、k≤3B、k3C、k=3D、k3
查看答案
考题 设n为正整数。则下面程序段的时间复杂度为()。 i=1;k=0; while(i A.O(1)B.O(nC.O(nlogn)D.O(n2)
查看答案
考题 设根结点的层次为O，则高度为k的完全二叉树的最小结点数为______。
查看答案
考题 设A为可逆矩阵，则下列结论不正确的是( )。A、(A-1)-1=A B、|A-1|=|A|-1 C、(KA)-1=KA-1(k≠0) D、(A')-1=(A-1)'
查看答案
考题 设A为可逆矩阵，k≠O，则下述结论不正确的是（ ）.
查看答案
考题 设A,B为n阶对称矩阵,下列结论不正确的是().A.AB为对称矩阵 B.设A,B可逆,则A^-1+B^-1为对称矩阵 C.A+B为对称矩阵 D.kA为对称矩阵
查看答案
考题 设A为n阶矩阵,k为常数,则(kA)+等于().
查看答案
考题 设三阶矩阵A的特征值为λ1=1,λ2=0,λ3=1,则下列结论不正确的是().A.矩阵A不可逆 B.矩阵A的迹为零 C.特征值-1,1对应的特征向量正交 D.方程组AX=0的基础解系含有一个线性无关的解向量
查看答案
考题 设A是4×3矩阵,r(A)=3,则下列4个断言中不正确为( ).
查看答案
考题 设A,B皆为n阶矩阵,则下列结论正确的是().A.AB=O的充分必要条件是A=O或B-O B.AB≠O的充分必要条件是A≠0且B≠0 C.AB=O且r(A)=N,则B=O D.若AB≠0,则｜A｜≠0或｜B｜≠0
查看答案
考题 设A是m×s阶矩阵,B为s×n阶矩阵,则方程组BX=O与ABX=O同解的充分条件是().A.r(A)=s B.r(A)=m C.r(B)=s D.r(B)=n
查看答案
考题 设A,B是可逆矩阵，且A与B相似，则下列结论错误的是
查看答案
考题 设A为n阶矩阵,A^2=A,则下列结论成立的是().A.A=O B.A=E C.若A不可逆,则A=O D.若A可逆,则A=E
查看答案
考题 设A是n阶矩阵，且Ak=O(k为正整数)，则( )。A.A一定是零矩阵 B.A有不为0的特征值 C.A的特征值全为0 D.A有n个线性无关的特征向量
查看答案
考题 设A为n阶实对称矩阵,下列结论不正确的是().A.矩阵A与单位矩阵E合同 B.矩阵A的特征值都是实数 C.存在可逆矩阵P,使P^-1AP为对角阵 D.存在正交阵Q,使Q^TAQ为对角阵
查看答案
考题 设A为n阶矩阵,下列结论正确的是().
查看答案
考题 设A=,B为三阶非零矩阵,且AB=O,则r(A)=_______.
查看答案
考题 设A为n阶对称矩阵，k为常数.试证kA仍为对称矩阵.
查看答案
考题 设A为n阶非零矩阵,且存在自然数k,使得A^k=O.证明：A不可以对角化.
查看答案
考题 设A为s×n矩阵且A的行向量组线性无关，K为r×s矩阵。证明：B＝KA行无关的充分必要条件是R(K)=r
查看答案
考题 设A=,且存在三阶非零矩阵B,使得AB=O,则a=_______,b=_______.
查看答案
考题 设B≠O为三阶矩阵,且矩阵B的每个列向量为方程组的解,则k=_______,｜B｜=_______.
查看答案
考题 设A为四阶实对称矩阵，且A^2+A=O.若A的秩为3，则A相似于
查看答案
考题 设n阶矩阵A可逆，α是A的属于特征值λ的特征向量，则下列结论中不正确的是( )。 A. α是矩阵-2A的属于特征值-2λ的特征向量 D. α是矩阵AT的属于特征值λ的特征向量
查看答案
考题 设A为4阶方阵，|A|-a≠0，则下列结论不正确的是（）。
查看答案
热门标签
最新试卷