网友您好, 请在下方输入框内输入要搜索的题目:
题目内容
(请给出正确答案)
如右图所示,在△ABC:中,D为AC的中点,E在BC上,且 BE : EC=1 : 2,AE与BD交于F。则△BEF与四边形EFDC 的面积之比为( )。
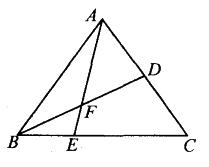
A. 1 : 3 B. 1 : 4
C. 1 : 5 D. 1 : 6

A. 1 : 3 B. 1 : 4
C. 1 : 5 D. 1 : 6
参考答案
参考解析
解析: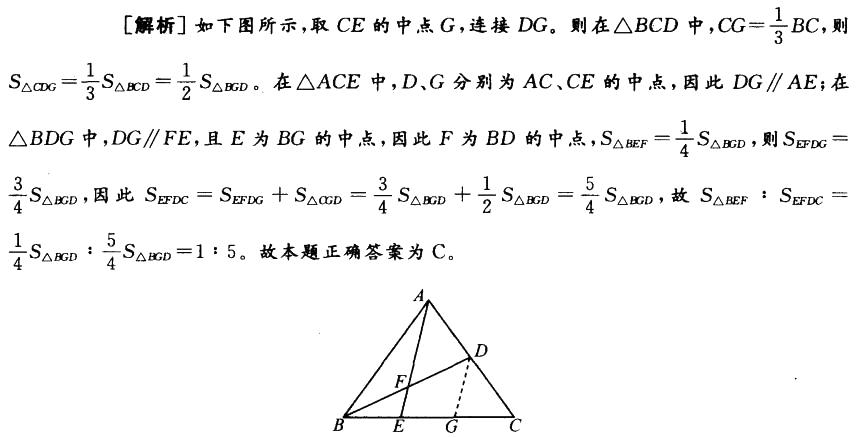

更多 “如右图所示,在△ABC:中,D为AC的中点,E在BC上,且 BE : EC=1 : 2,AE与BD交于F。则△BEF与四边形EFDC 的面积之比为( )。 A. 1 : 3 B. 1 : 4 C. 1 : 5 D. 1 : 6” 相关考题
考题
如右图,正四面体P-ABC的棱长为口,D、E、F分别为棱PA、PB、PC的中点,G、H、M分别为DE、EF、FD的中点,则三角形GHM的面积与正四面体P-ABC的表面积之比为:A.1:8B.1:16C.1:32D.1:64
考题
一块三角形农田ABC(如下图所示)被DE、EF两条道路分为三块。已知BD=2AD,CE=2AE,CF=2BF,则三角形ADE、三角形CEF和四边形BDEF的面积之比为:
A.1∶3∶3
B.1∶3∶4
C.1∶4∶4
D.1∶4∶5
考题
如图,D是△ABC内的一点,BD⊥CD,AD=6,BD=8,CD=6,E,F,G,H分别是AB,AC,CD, BD的中点.则四边形EFGH的周长是()。
A.12
B.14
C.15
D.16
考题
如右图,在梯形ABCD中,点E、F分别是腰AB、CD上的点.
(1)证明:如果E、F为中点时,有 EF=1/2(AD+BC);
(2)请写出(1)中命题的逆命题,并判断该逆命题是否成立,若成立,请给予证明;若不成立,请说明理由.
考题
如右图所示,梯形ABCD的对角线AC⊥BD,其中AD=1/2,BC=3,AC=14/5 ,BD=2.1.问梯形ABCD的高AE的值是:
A. 43/24
B. 1.72
C. 42/25
D. 1.81
考题
平行四边形ABCD如右图所示,E为AB上的一点,F、G分别是AC和DE、DB的交点。若AB=3AE,则四边形BEFG与ABCD的面积之比是:
A.2︰7
B.3︰13
C.4︰19
D.5︰24
考题
如右图所示,△ABC是等腰直角三角形,AB=12,AD的长度是CD的2倍,四边形EBCD与△AED的面积之比为3:2,问AE的长度是多少( )
A.6.9 B.7.1 C.7.2 D.7.4
考题
人行道ABC,BC长286cm,D为BC中点。AD直线距离为324cm,过B点做直线BE,过C点做垂线与BE交于E点,问AE最小距离为多少?
A.38cm
B.168cm
C.176cm
D.181cm
考题
如图所示,在长方形ABC.D中,AD=2AB,E为BC.的中点,F为EC.上任意一点(与E点、C.点不重合),从图形6个点中随机选取3个,能构成直角三角形的概率为:
A.1/2
B.9/20
C.7/20
D.2/5
考题
(10分)如图,几何体A1B1C1-ABC中,AB=AC,AB⊥AC,棱AA1,BB1,CC1都垂直于面ABC,BC=AA1=2BB1=2CC1=4,D为B1C1的中点,E为A1D的中点。
求证:(1)AE⊥BC;(3分)
(2)求异面直线AE与DC所成角的余弦值。(7分)
考题
圆内接四边形ABCD的一组对边AD、BC的延长线相交于户,对角线AC、BD相交于Q点,则图中共有相似三角形()。A、4对B、2对C、1对D、3对
热门标签
最新试卷